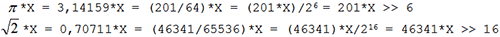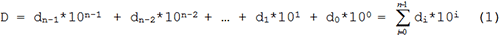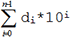В данной главе речь пойдёт о преобразовании числовых величин из одной формы представления в другую. Наряду с арифметическими операциями данный аспект программирования является основополагающим.

Большая часть информации в электронно-вычислительной системе всегда представлена в позиционном двоичном коде. Система команд любого микропроцессора напрямую поддерживает числа только такого типа. Для взаимодействия с пользователем (когда необходима визуализация или ввод/вывод информации) используется более привычная десятичная система исчисления, что приводит к необходимости отображать в памяти такие данные в виде двоично-кодированных десятичных цифр (двоично-десятичном коде). Помимо этого существует ещё множество других форматов, которые необходимы для реализации интерфейса с разного рода периферийными узлами (микросхемами памяти, логики, датчиками и т.д.). Во всех этих случаях задача преобразования требует частных способов решения.

Изменение масштаба числовых величин

В вычислениях часто приходится умножать числа на какой-либо фиксированный коэффициент. Если этот коэффициент является целочисленной величиной, то проблем не возникает (используется операция целочисленного умножения). Но бывает и так, что константа число иррациональное. Для того чтобы избежать использования арифметики с фиксированной или плавающей запятой, нужно представить иррациональную константу k в виде обыкновенной правильной/неправильной дроби

 k = a/b.

В этом случае действие умножения на дробное число k будет сведено к двум целочисленным операциям умножения на числитель a и деления на знаменатель b.

Вычисления могут быть заметно упрощены, если в качестве b выбрать число кратное целой степени 2. Тогда процедуру деления можно будет свести к простому сдвигу делимого вправо на соответствующее число разрядов:

В таких расчётах нужно обращать внимание на очерёдность выполнения арифметических операций. Первой всегда должна следовать операция умножения, а уже за ней деление. После целочисленного деления в общем случае образуется остаток, который, если его не учитывать, вносит в процесс вычислений систематическую погрешность δ. В дальнейших расчётах эта погрешность может многократно возрасти и изменить результат до неузнаваемости. При умножении целого числа X на дробь a/b получим

 (X/b + δ)*a = X*(a/b) + a*δ.

На этапе деления была получена абсолютная погрешность δ, которая в итоге возросла в a раз. В тоже время подобного рода погрешность не увеличится, если деление и умножение поменять местами   

(X*a)/b = X*(a/b) + δ.

Чем позднее в вычислениях (в порядке следования математических операций) будет внесена погрешность – тем точнее результат будет получен.

Что же касается точности, с которой должен быть представлен множитель k, то, при желании, она может быть сколь угодно велика при соответствующем подборе a и b. Только не всегда стоит к этому стремиться. Если программа обрабатывает n-разрядные данные прототипом, которых являются реально измеренные физические величины, то относительная погрешность их представления не может быть, ниже 1/2n. Это связано как с дискретностью измерений, так и с ограниченной точностью любых измерительных приборов. В этом случае вполне достаточно иметь точность представления k такого же порядка. При использовании встроенного аналого-цифрового преобразователя, разрешение которого составляет 10 значащих разрядов (минимальная относительная погрешность 1/210 ≈ 0,1%), не имеет смысла для умножения результата, например, на k = π/2 √2 ≈ 1,11072… брать больше одного - двух разрядов после запятой (т.е. брать k c точностью более 0,1%).

Преобразование из десятичной системы в двоичную

Самый очевидный способ десятично-двоичного преобразования вытекает непосредственно из формы записи десятичного числа:

Необходимо просто найти сумму 

по заданным коэффициентам di. Ниже приведена подпрограмма, преобразования десятичного 4-разрядного числа из диапазона 0…9999 в его двоичный 2-байтовый эквивалент 0…0x270F. Преобразуемое число хранится в SRAM микроконтроллера в виде четырех двоично-кодированных десятичных цифр d4…d0.

Десятично-двоичное преобразование можно также произвести по схеме Горнера:

D = (…(dn-1*10 + dn-2)*10 + … + d1)*10 + d0 (2)

Такая запись десятичного числа позволяет использовать следующий алгоритм: старший разряд десятичного числа dn-1 умножается на 10 (основание системы), к нему прибавляется следующий разряд dn-2 и полученная сумма dn-1*10 + dn-2 снова умножается на 10 и т.д. Подпрограмма преобразования по схеме Горнера десятичного числа, лежащего в диапазоне 0…65535, в 2-байтовое 0…0xFFFF:

С точки зрения требуемых вычислительных ресурсов десятично-двоичные преобразования, проведенные по формулам (1) и (2), примерно равноценны. Оба алгоритма требуют по n-1 операций сложения и умножения. Однако за счёт того, что в схеме Горнера используется умножение на постоянный множитель 10, вместо серии умножений на 10, 100, 1000… , ее использование оказывается более предпочтительным для преобразования многоразрядных чисел (легче организовать умножение в цикле и меньше команд уходит на подготовку множителя).

Преобразование из двоичной системы в десятичную

Двоично-десятичное преобразование встречается на практике чаще, чем десятично-двоичное, но реализуется немного сложнее. Приходится решать обратную задачу определения десятичных коэффициентов по известному двоичному полиному.

В соответствии с (1) все коэффициенты di (разряды десятичного числа, подлежащие определению) могут быть найдены последовательным делением D на 10i. Так после первого деления D/10n-1 получим старший разряд dn-1 как частное и остаток от деления dn-2*10n-2 + … + d1*101 + d0*100. Потом делением остатка на 10n-2 получим очередной разряд dn-2 и т.д.

Подпрограмма  преобразования однобайтового двоичного числа в 3-разрядное десятичное приведена ниже. В ней пришлось использовать две операции деления на 100 и на 10.

Преобразование однобайтовых чисел по (1), как мы видим, вполне оправдано. Но если понадобиться перевести в десятичное представление, например, 3-байтовое двоичное число, то необходимо будет использовать несколько подпрограмм деления на 10,100,1000 и т.д. Схема Горнера же позволяет обойтись только делением на 10, не зависимо  от размера преобразуемого числа.

Первое деление D из (2) на 10 даст самый младший разряд d0 в виде остатка и частное …(dn-1*10 + dn-2)*10 + … + d1. Произведя деление, полученного в предыдущем цикле частного, на 10, определяем следующий по старшинству разряд d1 и т.д. Определение коэффициентов di по схеме Горнера, в отличии от (1), ведется от младшего разряда d0 к старшему dn-1.

Подпрограмма преобразования 2-байтового двоичного числа в 5-разрядное десятичное (десятичные коэффициенты d4…d0 хранятся в SRAM микроконтроллера):

Для двоично-десятичного преобразования существует еще один алгоритм, связанный с использованием двоично-десятичной коррекции результата. По сравнению с приведёнными выше примерами, он требует больших затрат памяти программ и регистров но выполняется с наибольшей скоростью.

Процессор производит все арифметические операции по законам двоичной арифметики и поэтому интерпретирует любые данные именно как двоичные числа. Соответственно, результатом таких операций также являются числа, представленные в двоичном формате. Если используется какая либо иная форма представления чисел, то почти наверняка, любые действия, произведённые над ними, приведут к ошибке. Это произойдёт по тому, что числа, записанные в другом коде (отличном от позиционного), подчиняются и иным математическим законам.

Допустим, мы хотим сложить два однобайтовых двоично-десятичных числа 0x95 и 0x76, которые представляют собой запись десятичных чисел 95 и 76 соответственно (в младших полубайтах записано число единиц, в старших - число десятков), и получить сумму 0x171 (7 десятков, 1 единица, установленный флаг переноса C как сотня) представленную также в двоично-десятичном формате. Однако, после выполнения команды add Rd,Rr будет получено число 0x10B (0x0B и установленный флаг переноса C) и это полностью законный результат с точки зрения двоичной арифметики.

У многих микропроцессоров существует специальная команда, которая осуществляет коррекцию результата сложения, если слагаемые были представлены в двоично-десятичном формате. В нашем случае такая команда преобразовала бы сумму 0x10B в 0x171. Однако у AVR-микроконтроллеров такая инструкция, к сожалению, отсутствует. Тем не менее, двоично-десятичную коррекцию можно легко реализовать программным способом.

Использование двоично-десятичной коррекции совместно с вычислительной схемой Горнера позволяет преобразовать двоичные числа в следующей последовательности:

B = (…(bn-1*2 + bn-2)*2 + … + b1)*2 + b0.

К произведению bn-1*2 прибавляем следующий справа двоичный разряд bn-2 и посредством двоично-десятичной коррекции преобразуем двоичную сумму bn-1*2 + bn-2 в двоично-десятичную форму представления. На следующем этапе точно также производится умножение (bn-1*2 + bn-2)*2 и, после прибавления разряда bn-3, сумма (bn-1*2 + bn-2)*2 + bn-3 снова подлежит коррекции и т.д.

Следующая подпрограмма осуществляет преобразование двоичного трёхбайтового числа, лежащего в диапазоне 0…0xFFFFFF, в десятичное (0…16777215). Вместо серии умножений bn-1*2, (bn-1*2 + bn-2)*2, … в нём используется сдвиг накопителя суммы на 1 разряд влево.

Преобразование рефлексного кода в позиционный двоичный

Очень редко может возникнуть необходимость в преобразовании чисел, представленных в рефлексном коде (коде Грея) в позиционный код. В приложениях на основе микроконтроллеров данные в коде Грея могут поступать от некоторых датчиков старого типа.

Для преобразования числа B, представленного в позиционном двоичном коде, в число G записанное в двоичном рефлексном коде необходимо произвести операцию “исключающее ИЛИ” между самим числом B и частным, полученным от деления B/2:

G = B ^ (B/2) = bn-1*2n-1 + (bn-2^bn-1)*2n-2 + … + (b2^b1)*21 + b1^b0

Преобразование из рефлексного кода в позиционный (сводится к последовательному определению разрядов bn двоичного числа). Как видно, старший коэффициент bn-1 в позиционном двоичном и рефлексном кодах всегда совпадают. Для определения bn-2 необходимо произвести битовую операцию bn-1^(bn-2^bn-1). Точно также по известному bn-2 определяется bn-3 = bn-2^(bn-3^bn-2) и т.д. Подпрограмма преобразования 16-разрядного числа в коде Грея в его двоичный эквивалент: