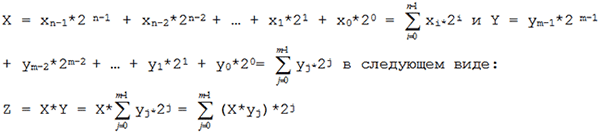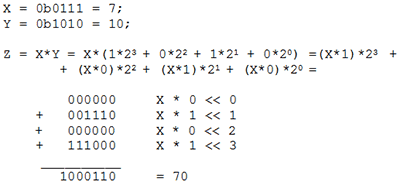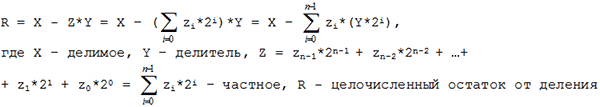|
||||||||||||||||||||||||||||||||||||
|
Программирование математических операций на Ассемблере в AVR Studio
Время создания: 02.12.2021 17:34
Раздел: Компьютер - Программирование - Ассемблеры - Архитектура AVR - Ассемблер в AVR Studio
Запись: xintrea/mytetra_syncro/master/base/1638455672ledxemsbx2/text.html на raw.githubusercontent.com
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Беззнаковые целые числа Эта глава главным образом будет посвящена арифметическим операциям над большими беззнаковыми целыми числами (подробней о различных форматах чисел смотри в приложении Б). В приложениях на AVR-микроконтроллерах наиболее часто приходится использовать 16-разрядные вычисления, которые достаточно легко программируются. Двухбайтовые числа предоставляют достаточно широкий диапазон представления переменных. Однако, встречаются задачи в которых необходимо применение чисел и с большей разрядностью (счётчики импульсов, накопители суммы, промежуточные результаты вычислений и т.д.). Сложение Реализовать многобайтовое сложение очень просто. Для этого имеется специальная команда adc Rd,Rr, которая складывает содержимое двух регистров и добавляет к полученной сумме бит переноса C из регистре SREG (Rd <- Rd+Rr+С). Этот бит устанавливается всегда, когда в результате предыдущей операции сложения возникает переполнение (т.е. бит C всегда является 9-ым битом результата операции сложения). Так может выглядеть сложение двух 16-разрядных чисел R17:R16 и R19:R18 (сумма размещается на месте второго слагаемого R19:R18):
Необходимо помнить, что в результате сложения двух n-разрядных чисел возможно образование n+1-разрядной суммы. Например, в результате следующей операции сложения получим: 0xB2FF + 0xCC45 = 0x17F44 = 0x10000 + 0x7F44. Сумма двухбайтовых слагаемых превысила максимальное 16-разрядное значение 0xFFFF = 65535 и вместо 0x17F44 = 98116 мы получили 0x7F44 = 32580. При этом должен установиться флаг C (17-тый разряд суммы), как признак того, что произошел перенос в старший разряд и к полученному результату необходимо добавить 0x10000 = 65536. В регистре SREG имеется еще один бит непосредственно связанный с действием сложения. Это флаг половинного переноса H, который может использоваться в 4-разрядных вычислениях. Он носит тот же смысл, что и флаг C, но указывает на переполнение суммы младших полубайтов (т.е. перенос из третьего в четвертый разряды числа). Флаг H почти никогда не используется на практике. Если для хранения результата вычисления не хватает РОНов, то сложение рационально производить с помощью косвенной адресации, а результат размещать в SRAM процессора. В этом случае разрядность слагаемых и вычисленной суммы будет ограничена только свободным местом в памяти данных. Подпрограмма такого сложения:
Вычитание Подобно сложению с переносом в архитектуре AVR существует и команда вычитания с заемом sbc Rd,Rr. Для связи байтов в ней тоже участвует флаг C, который в этом случае обычно называется флагом заема. Бит C устанавливается каждый раз, когда результат предыдущей операции вычитания оказывается меньше нуля и автоматически вычитается из разности полученной после команды sbc Rd,Rr (Rd <- Rd-Rr-С). Ниже показан пример вычитания 16-разрядного числа R17:R16 из R19:R18 (разность помещается на место вычитаемого):
Разрядность разности при вычитании никогда не превысит разрядности делимого. Однако здесь возникает другая проблема, связанная с тем, что уменьшаемое может оказаться меньше вычитаемого. В результате такого действия мы получим установленный флаг C, как признак отрицательного результата. И хотя с точки зрения арифметики такая операция является вполне законной - она приводит к отрицательным числам, представленным в дополнительном коде, которые будут рассмотрены в следующем разделе. Ниже приведена подпрограмма вычитания двух многобайтовых чисел, размещенных в SRAM.
Умножение У микроконтроллеров AVR, по сути, имеется два пути реализации умножения, разница между которыми заключается в форме представления произведения и, соответственно, в различии выполняемых арифметических операций. Первый оптимизирован для использования с командой однобайтового умножения, второй – использует только сложение и сдвиговые операции. Для произведения n-разрядного множимого и m-разрядного множителя необходимо отводить n+m разрядов. Помимо этого существует особый случай умножения на целую степень 2. Всё дело в том, что 2 является основанием двоичной системы, а в любой позиционной системе операция умножения числа на основание системы приводит к увеличению веса каждого его разряда на порядок: 2*X = 2*(xn-1*2n-1 + xn-2*2n-2 + … + x1*21 + x0*20) = xn-1*2n + xn-2*2n-1 + … + x1*22 + x0*21. Как видно, коэффициенты xn числа X переместились на один разряд влево (x0 стал при 21, x1 стал при 22 и т.д.). Итак, для умножения двоичного числа на 2n необходимо просто сдвинуть его на n разрядов влево. Так можно осуществить умножение на 2 двухбайтового числа в регистрах R17:R16 посредством сдвиговых операций:
Тот же результат можно получить, складывая число с самим собой:
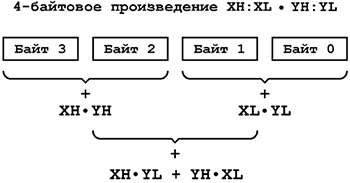
Благодаря тому, что операции сдвига и сложения выполняются за одинаковое время (1 машинный цикл) оба примера равноценны. Иногда встречаются операции умножения на число, которое близко к степени 2. В таких случаях намного проще заменить его суммой двух слагаемых, одно из которых кратно 2n, и использовать только операции сдвига и сложения (вычитания): 63*X = (26-1)*X = 26*X - X = X<<6 – X, 33*X = (25+1)*X = 25*X + X = X<<5 + X, 130*X = (27+2)*X = 27*X + 2*X = X<<7 + X<<2. Для умножения 2-байтовых чисел (обозначим их как XH:XL = 28*XH + XL и YH:YL = 28*YH + YL) применяется следующая вычислительная схема: XH:XL * YH:YL = (28*XH + XL)*(28*YH + YL) = 216*XH*YH + 28*(XH*YL + YH*XL) + XL*YL.
Рис.1 Вычислительная схема для умножения двухбайтовых чисел с использованием инструкции умножения Отыскание 32-разрядного результата сводится к последовательности операций однобайтовых умножений и последующего сложения всех произведений с учётом сдвига слагаемых XH*YL, XL*YH на 1 байт и XH*YH на 2 байта, как показано на рис.1. Подпрограмма, реализующая эти действия, приведена ниже. Напомним, что произведение двух однобайтовых множителей, полученное в результате выполнения команды mul Rd,Rr или любой другой команды умножения, всегда заносится в регистровую пару R1:R0.
Возвести двухбайтовое число в квадрат еще проще:
XH:XL * XH:XL = (28*XH + XL)*(28*XH + XL) = 216*XH*XH + 28*2*XH*XL + XL*XL. Подпрограмма возведения в квадрат приведена ниже. Она является хорошим примером того, где может пригодиться инструкция fmul Rd,Rr, которая одним действием производит умножение двух однобайтовых чисел и сдвиг произведения на 1 разряд влево.
Во многих случаях команда fmul Rd,Rr позволяет использовать аппаратный умножитель 8x8 фактически как умножитель 9x8 с получением 17-разрядного результата (MSB произведения размещается в C). Это бывает очень полезно, когда возникает необходимость умножить переменную на постоянный числовой коэффициент, который немного выходит за пределы 8-разрядной сетки. Так, допустим, можно умножить число из R16 на 500
или на 1000:
Ниже показан другой практически важный пример умножения, когда один из множителей (множитель X) однобайтовый. В основе подпрограммы лежит следующая вычислительная схема: X * YH:YL = X*(28*YH + YL) = 28*X*YH + X*YL
Точно также могут быть разложены числа и с большей разрядностью. Однако с ростом их величины начинают резко возрастать и затраты ресурсов процессора. Так для умножения трёхбайтовых чисел понадобится по 9 операций однобайтовых умножений и двухбайтовых сложений; для четырёхбайтовых уже по 16 операций и т.д. В подобных случаях необходимо использовать другой, наиболее общий алгоритм, который не использует команду mul Rd,Rr. А для микроконтроллеров семейства ATtiny, (а также для устаревшей линейки моделей Classic), у которых отсутствует аппаратный умножитель, он вообще является единственно возможным. Для пояснения алгоритма, перепишем произведение Z двух произвольных двоичных чисел
Произведение X*yj называется частичным произведением (X*yj = X при yj =1 и X*yj = 0 при yj =0), а произведение (X*yj)*2j есть не что иное, как частичное произведение, сдвинутое на j разрядов влево. Итак, нахождение произведение X*Y сводится к нахождению суммы частичных произведений X*yj, каждое из которых в свою очередь сдвинуто на j разрядов влево соответственно. На этом принципе основан школьный метод умножения в столбик. Рассмотрим пример умножения двух 4-разрядных чисел:
Как видим, для получения результата используются только операции сложения и сдвига. При этом в тех разрядах Y, где yj=0 и X*yj=0. И если предварительно анализировать значения yj/, то можно пропускать пустое сложение с 0 в соответствующих итерациях. Ниже приведена подпрограмма умножения двух трёхбайтовых чисел. В ней для получения суммы частичных произведений, сдвинутых каждое на j разрядов влево, производится сдвиг накопителя произведений m=24 раза вправо, а для экономии памяти младшие 3 байта произведения заносятся в те же регистры, где находился множитель.
Деление Из всех арифметических операций деление занимает особое место. По отношению к умножению деление является обратной операцией и не имеет конечной формулы для определения частного. Деление – единственная арифметическая операция ограниченной точности! Не смотря на это алгоритмы деления достаточно просты. Ниже будут показаны два таких алгоритма, которые используют только операции вычитания и сдвигов. Для того чтобы получить результат в виде целочисленных частного и остатка нужно предварительно убедиться в том, чтобы делимое было больше делителя и, конечно, исключить возникновение запрещённой операции деления на 0. При делении n-разрядного делимого на m-разрядный делитель под частное необходимо отвести n, а под остаток m разрядов. Частным случаем является деление на целую степень 2: X/2 = (x-1*2n-1 + xn-2*2n-2 + … + x1*21 + x0*20 )/2 = xn-1*2n-1 + xn-2*2n-2 + … + x1*20 + x0*1/21 Все коэффициенты xn двоичного числа X переместились на один разряд вправо (x0 стал при 1/21, x1 стал при 20 и т.д.). Таким образом для деления двоичного числа на 2n необходимо произвести сдвиг его содержимого на n разрядов в правую сторону. Так выглядит деление на 2 16-разрядного числа в регистрах R17:R16:
Обратите внимание на то, что после сдвига вправо во флаге переноса С окажется целочисленный остаток (младший коэффициент x0) от деления на 2. Для другого частного случая деления на 3 существует один очень интересный алгоритм, основанный на разложении дроби X/3 в ряд вида: X/3 = X/2 - X/4 + X/8 - X/16 + X/32 - … Каждый член ряда получается делением X на целую степень 2, что как было показано выше, легко реализуется сдвиговыми операциями. Ниже приведена подпрограмма деления на 3 16-разрядного числа.
Этот пример очень эффективен. Его быстродействие ограничено только разрядностью делимого. Более того для делимого произвольной величины обрабатывается оптимальное число членов ряда (до 16), а результат автоматически округляется до ближайшего целого числа. Естественно, что в тех случаях, когда необходимо разделить число на 6 можно совместно использовать приемы деления на 2 и 3: X/6 = (X/2)/3 = (X >> 1)/3 = (X/3) >> 1 Для уменьшения погрешности деление чётных чисел следует начинать с деления на 2 (остаток 0) а, деление нечётных с деления на 3 (алгоритм этого вида деления учитывает остаток). В общем случае самый естественный и простой способ разделить одно число на другое – это решить уравнение, вытекающее непосредственно из определения операции деления: X = Z*Y + R, R < Y, Y ≠ 0, где X – делимое, Y – делитель, Z – частное, R – целочисленный остаток от деления. Уравнение содержит два неизвестных параметра Z и R и поэтому не может быть явно разрешено. Для отыскания результата необходимо прибегнуть к итерационному методу: вычитать из делимого делитель до тех пор, пока остаток не окажется меньше делителя. Тогда число циклов вычитания численно даст частное Z, а остаток будет равен целочисленному остатку R от деления. Для примера, произведем следующее деление: X = 213, Y = 10, X - Z*Y = R, 213 – 21*10 = 3, Z = 21, R = 3. Мы 21 раз смогли вычесть из 213 по 10 пока не образовался остаток 3<10. Приведённый алгоритм имеет существенный недостаток – скорость его выполнения напрямую зависит от величины частного (числа итераций вычитания), что делает нежелательным его использование для деления больших чисел. Применяется он, в основном, в задачах ограниченных делением однобайтовых величин. Подпрограмма деления:
Для чисел большей разрядности необходимо использовать способ деления, основанный на приведенной ниже вычислительной схеме. Для этого представим необходимо выражение операции деления в следующем виде:
Нахождение частного сводится к отысканию его коэффициентов zi, которые определяются, согласно формуле, следующим образом: необходимо последовательно сравнивать X с произведениями Y*2i и если X > Y*2i, то в этом случае необходимо произвести вычитание Y*2i из X, а соответствующий разряд zi установить в 1; если X < Y*2i – вычитание пропускается и в этой итерации zi=0. Эта процедура продолжается до тех пор, пока не останется остаток Ri получаются простым сдвигом Y на i разрядов влево. Аналогично производится деление в любой позиционной системе (метод деления в столбик), но проще всего в двоичной из-за того, что в X может содержаться Y*2i максимум один раз (на что и указывает единица в соответствующем разряде). Рассмотрим пример деления:
Необходимо обратить внимание на то, что число итераций сравнения должно совпадать с числом значащих разрядов частного (в данном случае n=4 для определения z0…z3). Однако разрядность частного заранее никогда не известна и поэтому всегда необходимо знать максимально возможную разрядность результата деления. На практике чаще всего используют вычисления, в которых частное заведомо умещается в 8,16,24 бита (кратно одному байту) и т.д. При этом нужно использовать 8,16,24 итераций сравнения X с Y*2i, соответственно. С целочисленным остатком R проблем не возникает – его размер ограничен разрядностью Y (R < Y). Подпрограмма деления двухбайтового числа на однобайтовое приведена ниже. В ней для сравнения X с Y*2i (i ∈ {0,…,15}) вместо сдвига делителя Y на n разрядов вправо используется поочерёдный сдвиг делимого на n разрядов влево, а для экономии памяти частное записывается на тоже место, что и делимое. В начале программы осуществляется проверка условия Y ≠ 0, без которого деление не может быть корректно осуществлено.
Ниже приведена еще одна важная подпрограмма, реализующая деление 4-хбайтового числа на двухбайтовое с получением 16-разрядных частного и остатка. По своей структуре она аналогична предыдущей, кроме того, что при входе в подпрограмму производится проверка на переполнение результата и тем самым исключаются случаи, при которых частное может не умещаться в отведённых 2-х байтах (например, X = 0x51F356D, Y = 0x100, R = 0x6D, Z = 0x51F35 – имеет разрядность более 16 бит).
Формы представления частного в операциях деления Все подпрограммы деления, приведенные в предыдущем разделе, возвращают на выходе результат в виде целочисленных частного Z и остатка R X = 11, Y = 4, X/Y = Z + R, 11/4 = [2] + {3}. Однако при попытке продолжить деление, по аналогии с подобным действием в десятичной системе, что иногда бывает необходимо на практике, мы получим частное, представленное в форме дробного числа с фиксированной запятой X = 11, Y = 4, X/Y = Z + R, 11/4 = 0b10.11 Работа с такими числами ни чем не отличается от работы с неотрицательными целыми числами. Разница состоит лишь в том – где фиксируется дробная часть результата. Так результат деления 11/4 дал целую часть числа 2 и дробную (отделённые младшие два разряда) 0.75. Теперь если вам потребуется использовать этот результат в последующих арифметических операциях, то нужно просто запомнить где находится разделяющая запятая и соответственно определить веса каких разрядов 2n, а каких 1/2m. Тоже число 0b1011 может трактоваться по-разному в зависимости от того сколько разрядов отведено под целую и дробную части 0b1.011 = 1*20 + 0*(1/21) + 1*(1/22) + 1*(1/23) = 1.375 (формат (1.3)), 0b10.11 = 1*21 + 0*20 + 1*(1/21) + 1*(1/22) = 2.750 (формат (2.2)), 0b101.1 = 1*22 + 0*21 + 1*20 + 1*(1/21) = 5.500 ( формат (3.1)) и т.д. Рассмотрим как можно, например, сложить два дробных числа, предварительно приведя их к одному виду: 11/4 + 7/8 = 0b1011/0b0100 + 0b0111/0b1000 = 0b1011 >> 2 + 0b0111 >> 3 = 0b10.11 + 0b0.111 = 0b10.110 + 0b00.111 = 0b11.101 = 3.625 Дробные двоичные слагаемые 0b10.11 = 2.750 (формат (2.2)) и 0b0.111 = 0.875 (формата (1.3)) были приведены к единому формату представления (2.3) (0b10.110, 0b00.111), где целую и дробную части отделяют запятая между третьим и четвёртым разрядами. После этого мы их сложили, как два обыкновенных семизначных числа. Итак, дробные числа с фиксированной запятой – подчиняются всем тем же законам двоичной арифметики, что и целые числа. В случае использования дробных чисел с фиксированной запятой в промежуточных вычислениях необходимо заранее ограничить разрядность дробной части результата. Это обусловлено тем, что при делении возможно образование бесконечных дробей, как допустим, 179/9 = 0b1001.100001… = 10.515625…. Округление двоичных чисел происходит точно так же, как и в десятичной системе исчисления. Если дробный остаток от деления ≥0.5 (т.е. если старший разряд в остатке, вес которого как раз 1/21, равен 1) или целочисленный остаток R≥0,5*Y , то частное Z округляется в большую сторону. Так при делении 9/2 = 0b100.1 = 4.5 необходимо учесть дробную часть 0.5 и округлить частное до 5, а, например, при делении 9/4 = 0b10.01 = 2.25 остаток 0.25 надо отбросить. Другим способом произвести корректировку частного можно, если добавить к нему 1/2. Тогда можно будет свободно отбросить остаток, поскольку округление в большую сторону будет происходить каждый раз, когда R≥0,5. Добавление 1/2 к частному равносильно добавлению перед делением к делимому половины делителя (X + Y/2) / Y = X/Y + 1/2 = Z + 1/2. Подпрограмма, приведенная ниже вносит такую поправку перед делением 15-разрядного делимого на 8-разрядный делитель.
|
||||||||||||||||||||||||||||||||||||
|
Так же в этом разделе:
|
||||||||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|