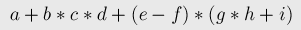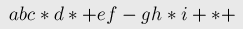Дана строка, представляющая собой математическое выражение, содержащее числа, переменные, различные операции. Требуется вычислить его значение за O(n), где n — длина строки.

Здесь описан алгоритм, который переводит это выражение в так называемую обратную польскую нотацию (явным или неявным образом), и уже в ней вычисляет выражение.

Обратная польская нотация

Обратная польская нотация — это форма записи математических выражений, в которой операторы расположены после своих операндов. Обратная польская нотация была разработана австралийским философом и специалистом в области теории вычислительных машин Чарльзом Хэмблином в середине 1950-х на основе польской нотации, которая была предложена в 1920 г. польским математиком Яном Лукасевичем.

Например, следующее выражение:

в обратной польской нотации записывается следующим образом:

Удобство обратной польской нотации заключается в том, что выражения, представленные в такой форме, очень легко вычислять, причём за линейное время. Заведём стек, изначально он пуст. Будем двигаться слева направо по выражению в обратной польской нотации; если текущий элемент — число или переменная, то кладём на вершину стека её значение; если же текущий элемент — операция, то достаём из стека два верхних элемента (или один, если операция унарная), применяем к ним операцию, и результат кладём обратно в стек. В конце концов в стеке останется ровно один элемент - значение выражения.

Очевидно, этот простой алгоритм выполняется за O(n), т.е. порядка длины выражения.

Разбор простейших выражений

Пока мы рассматриваем только простейший случай: все операции бинарны (т.е. от двух аргументов), и все левоассоциативны (т.е. при равенстве приоритетов выполняются слева направо). Скобки разрешены.

Заведём два стека: один для чисел, другой для операций и скобок (т.е. стек символов). Изначально оба стека пусты. Для второго стека будем поддерживать предусловие, что все операции упорядочены в нём по строгому убыванию приоритета, если двигаться от вершины стека. Если в стеке есть открывающие скобки, то упорядочен каждый блок операций, находящийся между скобками, а весь стек в таком случае не обязательно упорядочен.

Будем идти по строке слева направо. Если текущий элемент — цифра или переменная, то положим в стек значение этого числа/переменной. Если текущий элемент — открывающая скобка, то положим её в стек. Если текущий элемент — закрывающая скобка, то будем выталкивать из стека и выполнять все операции до тех пор, пока мы не извлечём открывающую скобку (т.е., иначе говоря, встречая закрывающую скобку, мы выполняем все операции, находящиеся внутри этой скобки). Наконец, если текущий элемент — операция, то, пока на вершине стека находится операция с таким же или большим приоритетом, будем выталкивать и выполнять её.

После того, как мы обработаем всю строку, в стеке операций ещё могут остаться некоторые операции, которые ещё не были вычислены, и нужно выполнить их все (т.е. действуем аналогично случаю, когда встречаем закрывающую скобку).

Вот реализация данного метода на примере обычных операций + - * / %:

bool delim (char c) {

return c == ' ';

}

 

bool is_op (char c) {

return c=='+' || c=='-' || c=='*' || c=='/' || c=='%';

}

 

int priority (char op) {

return

op == '+' || op == '-' ? 1 :

op == '*' || op == '/' || op == '%' ? 2 :

-1;

}

 

void process_op (vector<int> & st, char op) {

int r = st.back(); st.pop_back();

int l = st.back(); st.pop_back();

switch (op) {

case '+': st.push_back (l + r); break;

case '-': st.push_back (l - r); break;

case '*': st.push_back (l * r); break;

case '/': st.push_back (l / r); break;

case '%': st.push_back (l % r); break;

}

}

 

int calc (string & s) {

vector<int> st;

vector<char> op;

for (size_t i=0; i<s.length(); ++i)

if (!delim (s[i]))

if (s[i] == '(')

op.push_back ('(');

else if (s[i] == ')') {

while (op.back() != '(')

process_op (st, op.back()), op.pop_back();

op.pop_back();

}

else if (is_op (s[i])) {

char curop = s[i];

while (!op.empty() && priority(op.back()) >= priority(s[i]))

process_op (st, op.back()), op.pop_back();

op.push_back (curop);

}

else {

string operand;

while (i < s.length() && isalnum (s[i])))

operand += s[i++];

--i;

if (isdigit (operand[0]))

st.push_back (atoi (operand.c_str()));

else

st.push_back (get_variable_val (operand));

}

while (!op.empty())

process_op (st, op.back()), op.pop_back();

return st.back();

}

Таким образом, мы научились вычислять значение выражения за O(n), и при этом мы неявно воспользовались обратной польской нотацией: мы расположили операции в таком порядке, когда к моменту вычисления очередной операции оба её операнда уже вычислены. Слегка модифицировав вышеописанный алгоритм, можно получить выражение в обратной польской нотаци и в явном виде.

Унарные операции

Теперь предположим, что выражение содержит унарные операции (т.е. от одного аргумента). Например, особенно часто встречаются унарный плюс и минус.

Одно из отличий этого случая заключается в необходимости определения того, является ли текущая операция унарной или бинарной.

Можно заметить, что перед унарной операцией всегда стоит либо другая операция, либо открывающая скобка, либо вообще ничего (если она стоит в самом начале строки). Перед бинарной операцией, напротив, всегда стоит либо операнд (число/переменная), либо закрывающая скобка. Таким образом, достаточно завести какой-нибудь флаг для указания того, может ли следующая операция быть унарной или нет.

Ещё чисто реализационная тонкость — как различать унарные и бинарные операции при извлечении из стека и вычислении. Здесь можно, например, для унарных операций вместо символа s[i] класть в стек -s[i].

Приоритет для унарных операций нужно выбирать таким, чтобы он был больше приоритетов всех бинарных операций.

Кроме того, надо заметить, что унарные операции фактически являются правоассоциативными — если подряд идут несколько унарных операций, то они должны обрабатываться справа налево (для описания этого случая см. ниже; приведённый здесь код уже учитывает правоассоциативность).

Реализация для бинарных операций + - * / % и унарных операций + -:

bool delim (char c) {

return c == ' ';

}

 

bool is_op (char c) {

return c=='+' || c=='-' || c=='*' || c=='/' || c=='%';

}

 

int priority (char op) {

if (op < 0)

return 4; // op == -'+' || op == -'-'

return

op == '+' || op == '-' ? 1 :

op == '*' || op == '/' || op == '%' ? 2 :

-1;

}

 

void process_op (vector<int> & st, char op) {

if (op < 0) {

int l = st.back(); st.pop_back();

switch (-op) {

case '+': st.push_back (l); break;

case '-': st.push_back (-l); break;

}

}

else {

int r = st.back(); st.pop_back();

int l = st.back(); st.pop_back();

switch (op) {

case '+': st.push_back (l + r); break;

case '-': st.push_back (l - r); break;

case '*': st.push_back (l * r); break;

case '/': st.push_back (l / r); break;

case '%': st.push_back (l % r); break;

}

}

}

 

int calc (string & s) {

bool may_unary = true;

vector<int> st;

vector<char> op;

for (size_t i=0; i<s.length(); ++i)

if (!delim (s[i]))

if (s[i] == '(') {

op.push_back ('(');

may_unary = true;

}

else if (s[i] == ')') {

while (op.back() != '(')

process_op (st, op.back()), op.pop_back();

op.pop_back();

may_unary = false;

}

else if (is_op (s[i])) {

char curop = s[i];

if (may_unary && isunary (curop)) curop = -curop;

while (!op.empty() && (

curop >= 0 && priority(op.back()) >= priority(curop)

|| curop < 0 && priority(op.back()) > priority(curop))

)

process_op (st, op.back()), op.pop_back();

op.push_back (curop);

may_unary = true;

}

else {

string operand;

while (i < s.length() && isalnum (s[i])))

operand += s[i++];

--i;

if (isdigit (operand[0]))

st.push_back (atoi (operand.c_str()));

else

st.push_back (get_variable_val (operand));

may_unary = false;

}

while (!op.empty())

process_op (st, op.back()), op.pop_back();

return st.back();

}

Стоит заметить, что в простейших случаях, например, когда из унарных операций разрешены только + и -, правоассоциативность не играет никакой роли, поэтому в таких ситуациях никаких усложнений в схему можно не вводить. Т.е. цикл:

while (!op.empty() && (

curop >= 0 && priority(op.back()) >= priority(curop)

|| curop < 0 && priority(op.back()) > priority(curop))

)

process_op (st, op.back()), op.pop_back();

Можно заменить на:

while (!op.empty() && priority(op.back()) >= priority(curop))

process_op (st, op.back()), op.pop_back();

Правоассоциативность

Правоассоциативность оператора означает, что при равенстве приоритетов операторы вычисляются справа налево (соотвественно, левоассоциативность - когда слева направо).

Как уже было отмечено выше, унарные операторы обычно являются правоассоциативными. Другой пример - обычно операция возведения в степень считается правоассоциативной (действительно, a^b^c обычно воспринимается как a^(b^c), а не (a^b)^c).

Какие отличия нужно внести в алгоритм, чтобы корректно обрабатывать правоассоциативность? На самом деле, изменения нужны самые минимальные. Единственное отличие будет проявляться только при равенстве приоритетов, и заключается оно в том, что операции с равным приоритетом, находящиеся на вершине стека, не должны выполнять раньше текущей операции.

Таким образом, единственные отличия нужно внести в функцию calc:

int calc (string & s) {

...

while (!op.empty() && (

left_assoc(curop) && priority(op.back()) >= priority(curop)

|| !left_assoc(curop) && priority(op.back()) > priority(curop)))

...

}

Примечание: в этой статье описана обратная польская нотация. Однако существует и прямая польская нотация. Парсер на C++, реализованный на основе прямой польской нотации, приведен в статье: Рабочий пример простого парсера математических выражений .