Я уже рассказывал о польской записи, а именно о постфиксной нотации, называемой “Обратная польская запись”. Сейчас я хочу рассмотреть другую нотацию – префиксную. Прямая польская запись – это алгебраическое выражение, записанное в префиксной (prefix) форме. Отличие префиксной формы от постфиксной заключается в том, что операторы пишутся перед операндами (а не после). Сходство же кроется в том, что операнды не меняют своего относительного расположения, зато меняется порядок следования операций и функций как по отношению к операндам, так и по отношению друг к другу. Посмотрим несколько примеров записи выражения в инфиксной и префиксной форме.
|
Инфиксная форма записи Префиксная форма записи
7 + ( 5 - 2 ) * 4 + 7 * - 5 2 4
8 / ( 2 + 2 ) ^ 2 / 8 ^ + 2 2 2
( 8 / ( 2 + 2 ) ) ^ 2 ^ / 8 + 2 2 2
( 2 + 5 * 4 ) / ( 8 / 2 – 2 ) / + 2 * 5 4 - / 8 2 2 | |
Для построения прямой польской записи я воспользуюсь методом рекурсивного спуска. Суть данного метода заключается в разделении основной задачи (в данном случае строки с формулой) на подзадачи (далее по тексту – простые формулы), и работе с ними. Простая формула – это формула, которая не содержит скобок. Краткий алгоритм действий таков (предполагается, что количество скобок в формуле сбалансировано). Разбираем строку, ища в ней крайнюю справа открывающую скобку. Если открывающей скобки нет – перед нами простая формула, строим для нее прямую польскую запись. Если скобка нашлась – выделяем простую формулу, вычисляем для нее прямую польскую запись, запоминаем результат и присваиваем ему псевдоним. Подставляем псевдоним в строку с формулой, не забывая удалить скобки. Продолжаем разбирать строку, пока не обработаем все простые формулы. Разберем этот алгоритм на следующем примере: (a+b)*(c–d). Первая итерация – находим крайнюю справа открывающую скобку и выделяем простую формулу:
Строим для нее прямую польскую запись и запоминаем. Присваиваем ей псевдоним и подставляем в строку с формулой:
|
// #1 = - c d
( a + b ) * #1 | |
Вторая итерация – находим крайнюю справа открывающую скобку и выделяем простую формулу:
Строим для нее прямую польскую запись и запоминаем. Присваиваем ей псевдоним и подставляем в строку с формулой:
|
// #1 = - c d
// #2 = + a b
#2*#1 | |
Третья итерация – открывающей скобки нет, значит осталась простая формула. Строим для нее прямую польскую запись и заканчиваем разбор строки:
|
// #1 = - c d
// #2 = + a b
// #3 = * #2 #1
#3 | |
Осталось собрать результат. Для этого последовательно перебираем все запомненные ранее псевдонимы, начиная с последнего, и подставляем в строку с формулой соответствующие им прямые польские записи: Первая итерация:
Вторая итерация:
Третья итерация:
Вот как это выглядит в коде (для упрощения разбора строки условимся, что все элементы формулы (операторы, операнды, скобки и функции) отделены друг от друга пробелом):
|
function MakePolish( const Formula: string ): string;
function PolishSimple( const SimpleFormula: string ): string;
begin
{...}
end;
var
TempFormula: string;
AliasReplacement, SimpleFormula: string;
BracketFound: Boolean;
OpenBracket, CloseBracket: Integer;
Iterator: Integer;
List: TStrings;
begin
TempFormula := Formula;
BracketFound := True;
Iterator := 0;
List := TStringList.Create;
while BracketFound do
begin
OpenBracket := LastDelimiter( '(', TempFormula );
if OpenBracket > 0 then
begin
CloseBracket := Pos( ')', TempFormula, OpenBracket );
Inc( Iterator );
AliasReplacement := Format( '#%d', [Iterator] );
List.Add( AliasReplacement + '=' +
PolishSimple( Trim( Copy( TempFormula, OpenBracket+1, CloseBracket-OpenBracket-1 ) ) ) );
TempFormula := Trim( Trim( Copy( TempFormula, 1, OpenBracket-1 ) ) + ' ' + AliasReplacement +
' ' + Trim( Copy( TempFormula, CloseBracket+1, Length( TempFormula ) ) ) );
end
else
BracketFound := False;
end;
SimpleFormula := PolishSimple( TempFormula );
while Iterator > 0 do
begin
AliasReplacement := Format( '#%d', [Iterator] );
Dec( Iterator );
SimpleFormula := StringReplace( SimpleFormula, AliasReplacement, List.Values[AliasReplacement], [] );
end;
List.Free;
Result := SimpleFormula;
end; | |
Теперь рассмотрим алгоритм обработки простой формулы и получения для нее прямой польской записи.
|
function PolishSimple( const SimpleFormula: string ): string;
const
SignArray: array[1..5] of Char = ( '+', '-', '*', '/', '^' );
var
TempFormula: string;
Op: Char; // Оператор
OpPos: Integer; // Позиция оператора
Polish: string; // Польская формула
i: Integer;
begin
for i := 1 to Length( SignArray ) do
begin
Op := SignArray[i];
OpPos := LastDelimiter( Op, SimpleFormula );
if OpPos > 0 then
begin
Polish := Op + ' ' + PolishSimple( Trim( Copy( SimpleFormula, 1, OpPos-1 ) ) ) + ' ' +
PolishSimple( Trim( Copy( SimpleFormula, OpPos+1, Length( SimpleFormula ) ) ) );
Break;
end;
end;
if Polish = '' then
Polish := SimpleFormula;
Result := Polish;
end; | |
Разберем работу этой функции на примере выражения 2+5*4–2. Функция разбивает строку на части, в качестве разделителя используются операторы, записанные в порядке увеличения их приоритета в константе SignArray. Поиск операторов производится слева направо, разбиение продолжается до тех пор, пока не будут перебраны все операторы в строке. Графически это можно представить так (скобками выделен оператор, использованный в качестве разделителя на каждой из итераций):
|
2 (+) 5 * 4 – 2
| |
2 5 * 4 (-) 2
| |
5 (*) 4 2
| |
5 4 | |
В результате разбиения будет построено дерево следующего вида (обратите внимание не операторы в вершинах узлов на каждом уровне - они соответствуют операторам, использованным в качестве разделителя на кождой из итераций):
|
+
/ \
2 -
/ \
* 2
/ \
5 4 | |
После построения дерева формируется прямая польская запись. Правило здесь простое – оператор, находящийся в вершине узла, становится слева, за ним записываются операторы в последовательности слева направо. В нашем дереве 3 узла, посмотрим, как поэтапно, в 3 шага, будет построена прямая польская запись: Первая итерация:
Вторая итерация:
Третья итерация:
Разумеется, скобок в польской записи не будет (их и не должно там быть). Я использовал их здесь исключительно для наглядности, заключая в них выражение, полученное на предыдущем этапе. Здесь я хочу сделать небольшое отступление и обратить ваше внимание на один момент. Операторы, участвующие в разборе строки должны быть обязательно указаны в порядке возрастания их приоритета. А вот последовательность операторов с одинаковым приоритетом не имеет принципиальной разницы с точки зрения расчета формулы, но влияет на формирование польской записи. Рассмотрим 2 примера:
|
function PolishSimple( SimpleFormula: string ): string;
const
SignArray: array[1..5] of Char = ( '+', '-', '*', '/', '^' );
{...}
begin
{...}
Result := Polish;
end;
ShowMessage( MakePolish( '2 + 5 * 4 - 2' ) ); | |
В результате мы получим выражение вида + 2 - * 5 4 2. А теперь поменяем местами первые 2 оператора.
|
function PolishSimple( SimpleFormula: string ): string;
const
SignArray: array[1..5] of Char = ( '-', '+', '*', '/', '^' );
{...}
begin
{...}
Result := Polish;
end;
ShowMessage( MakePolish( '2 + 5 * 4 - 2' ) ); | |
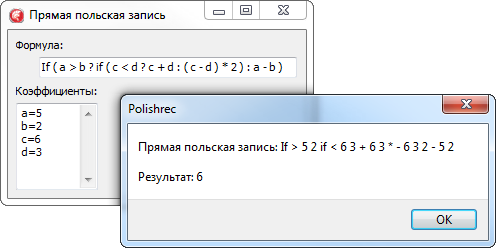
В этом случае польская запись будет иметь вид - + 2 * 5 4 2. Оба варианта польской записи корректны, так что определение порядка следования операторов с равным приоритетом – дело вашего личного вкуса. В качестве бонуса рассмотрим использование в формуле условного оператора If (такая задача стояла передо мной в одном из проектов, и подвигла на написание данной статьи). Синтаксис оператора я определил следующим образом: If ( условие ? True : False ). Работа с этим оператором не вызывает никаких затруднений, нужно лишь немного доработать функцию PolishSimple (об этом немного позже). А непосредственно при расчете, обрабатывая оператор If, извлекать из стека 3 операнда. Рассмотрим обработку этого оператора на примере формулы If(a>b?if(c<d?c+d:(c-d)*2):a-b). Прямая польская запись для этой формулы будет выглядеть следующим образом:
|
if > a b if < c d + c d * - c d 2 - a b | |
Проведем тестовый расчет, чтобы убедить в корректности и работоспособности данной записи. Входным коэффициентам присвоим следующие значения:
При таких входных параметрах на выходе мы должны получить результат выражения ( c - d ) * 2, т.к. первое условие выполняется, а второе нет.
|
( c - d ) * 2 => ( 6 - 3 ) * 2 = 6 | |
Расчет:
|
Итерация |
Формула |
Примечание |
|
0 |
if > 5 2 if < 6 3 + 6 3 * - 6 3 2 - 5 2 |
|
|
1 |
if > 5 2 if < 6 3 + 6 3 * - 6 3 2 3 |
|
|
2 |
if > 5 2 if < 6 3 + 6 3 * 3 2 3 |
|
|
3 |
if > 5 2 if < 6 3 + 6 3 6 3 |
|
|
4 |
if > 5 2 if < 6 3 9 6 3 |
|
|
5 |
if > 5 2 if 0 9 6 3 |
Проверка внутреннего условия (6 < 3) |
|
6 |
if > 5 2 6 3 |
Выполнение ветки False внутреннего условия |
|
7 |
if 1 6 3 |
Проверка внешнего условия (5 > 2) |
|
8 |
6 |
Выполнение ветки True внешнего условия |
Таким образом, окончательный вариант функции MakePolish выглядит так:
|
function MakePolish( const Formula: string ): string;
function PolishSimple( const SimpleFormula: string ): string;
const
SignArray: array[1..14] of Char = ( ',', '?', ':', '+', '-', '*', '/', '^', '>', '<', '=',
Chr( $2260 ), Chr( $2264 ), Chr( $2265 ) );
var
Op: Char; // Оператор
OpPos: Integer; // Позиция оператора
Polish: string; // Польская формула
i: Integer;
begin
for i := 1 to Length( SignArray ) do
begin
Op := SignArray[i];
OpPos := LastDelimiter( Op, SimpleFormula );
if OpPos > 0 then
begin
if CharInSet( Op, [',', '?', ':'] ) then
Polish := PolishSimple( Trim( Copy( SimpleFormula, 1, OpPos-1 ) ) ) + ' ' +
PolishSimple( Trim( Copy( SimpleFormula, OpPos+1, Length( SimpleFormula ) ) ) )
else
Polish := Op + ' ' + PolishSimple( Trim( Copy( SimpleFormula, 1, OpPos-1 ) ) ) + ' ' +
PolishSimple( Trim( Copy( SimpleFormula, OpPos+1, Length( SimpleFormula ) ) ) );
Break;
end;
end;
if Polish = '' then
Polish := SimpleFormula;
Result := Polish;
end;
var
TempFormula: string;
AliasReplacement, SimpleFormula: string;
BracketFound: Boolean;
OpenBracket, CloseBracket: Integer;
Iterator: Integer;
List: TStrings;
begin
TempFormula := Formula;
BracketFound := True;
Iterator := 0;
List := TStringList.Create;
while BracketFound do
begin
OpenBracket := LastDelimiter( '(', TempFormula );
if OpenBracket > 0 then
begin
CloseBracket := Pos( ')', TempFormula, OpenBracket );
Inc( Iterator );
AliasReplacement := Format( '#%d', [Iterator] );
List.Add( AliasReplacement + '=' +
PolishSimple( Trim( Copy( TempFormula, OpenBracket+1, CloseBracket-OpenBracket-1 ) ) ) );
TempFormula := Trim( Trim( Copy( TempFormula, 1, OpenBracket-1 ) ) + ' ' + AliasReplacement +
' ' + Trim( Copy( TempFormula, CloseBracket+1, Length( TempFormula ) ) ) );
end
else
BracketFound := False;
end;
SimpleFormula := PolishSimple( TempFormula );
while Iterator > 0 do
begin
AliasReplacement := Format( '#%d', [Iterator] );
Dec( Iterator );
SimpleFormula := StringReplace( SimpleFormula, AliasReplacement, List.Values[AliasReplacement], [] );
end;
List.Free;
Result := SimpleFormula;
end; | |
Символы с кодами $2260, $2264 и $2265 это ≠, ≤ и ≥ соответственно. Затруднений с расчетом возникнуть не должно. Пробегаемся по списку от конца к началу, и находя в нем оператор (или функцию) извлекаем соответствующее количество аргументов. Рассчитанное значение кладем обратно в список, на место оператора (или функции), а аргументы просто удаляем. В конце расчета в списке останется всего 1 элемент, значение которого и будет результатом. Вот как это может выглядеть:
|
function CalcPolish( const Polish: string ): Double;
var
List: TStrings;
i: Integer;
begin
List := TStringList.Create;
List.Delimiter := ' ';
List.DelimitedText := Polish;
Result := 0;
for i := List.Count-1 downto 0 do
begin
case List[i][1] of
'+', '-', '*', '/', '^', '>', '<', '=',
Chr( $2260 ), Chr( $2264 ), Chr( $2265 ):
begin
case List[i][1] of
'+': List[i] := FloatToStr( StrToFloat( List[i+1] ) + StrToFloat( List[i+2] ) );
'-': List[i] := FloatToStr( StrToFloat( List[i+1] ) - StrToFloat( List[i+2] ) );
'*': List[i] := FloatToStr( StrToFloat( List[i+1] ) * StrToFloat( List[i+2] ) );
'/': List[i] := FloatToStr( StrToFloat( List[i+1] ) / StrToFloat( List[i+2] ) );
'^': List[i] := FloatToStr( Power( StrToFloat( List[i+1] ), StrToFloat( List[i+2] ) ) );
'>': List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) > StrToFloat( List[i+2] ) ) );
'<': List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) < StrToFloat( List[i+2] ) ) );
'=': List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) = StrToFloat( List[i+2] ) ) );
Chr( $2260 ): List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) <> StrToFloat( List[i+2] ) ) );
Chr( $2264 ): List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) <= StrToFloat( List[i+2] ) ) );
Chr( $2265 ): List[i] := FloatToStr( Byte( StrToFloat( List[i+1] ) >= StrToFloat( List[i+2] ) ) );
end;
List.Delete( i+2 );
List.Delete( i+1 );
end;
else
if AnsiLowerCase( List[i] ) = 'if' then
begin
if StrToBool( List[i+1] ) then
List[i] := List[i+2]
else
List[i] := List[i+3];
List.Delete( i+3 );
List.Delete( i+2 );
List.Delete( i+1 );
end;
end;
end;
Result := StrToFloat( List[0] );
List.Free;
end;
procedure TForm1.Button1Click(Sender: TObject);
var
Polish: string;
i: Integer;
begin
Polish := MakePolish( Ed_Formula.Text );
for i := 0 to Memo1.Lines.Count do
Polish := StringReplace( Polish, Memo1.Lines.Names[i],
Memo1.Lines.Values[Memo1.Lines.Names[i]],
[rfReplaceAll, rfIgnoreCase] );
ShowMessage( 'Прямая польская запись: ' + Polish + #13#13 +
'Результат: ' + FloatToStr( CalcPolish( Polish ) ) );
end; | |
На этом все, спасибо за внимание! Успехов в программировании!
|





