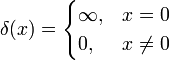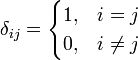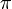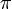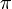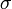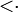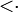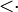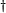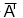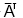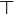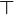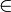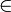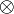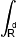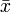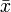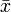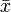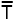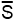В математике, для записей выражений, используется свой символьный язык, элементы которого проходят в школе.
Символ ∀ (перевёрнутая А) и ∃ (Е наоборот) — всего-навсего английские «Any» и «Exist», попавшие в «математический международный» таким идиотским способом из-за уже используемых «А» (альфа) и «Е» (число Эйлера). То есть:
- Символ ∀ (Any) используется для обозначения фразы «Для любого...», «Для любых...». Иногда такой знак называют "Квантор всеобщности".
- Символ ∃ (Exist) используется вместо слова «существует». Иногда такой знак называют "Квантор существования".
Далее:
- Символ Σ — это греческая буква «сигма». Означает сумму элементов.
- Символ ∏ - больша греческая буква «пи». Означает произведение элементов.
- Символ
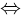 - обозначает равносильность. Например, - обозначает равносильность. Например, 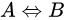 следует читать «A верно тогда и только тогда, когда B верно» следует читать «A верно тогда и только тогда, когда B верно»
- Символ ∈ - означает "принадлежит". Обычно используется в контексте множеств, т. е. обозначает "принадлежит множеству".
- Символ ∉ - буквально означает "не принадлежит".
- Символ ⋃ - от слова (union) - обозначает "объединение" того что слева от него и того что справа. Обычно используется в теории множеств.
- Символ ⋂ - обозначает "пересечение". В теории множеств используется для обозначения результата операции пересечения множества A и B: A ⋂ B.
Виды чисел:
- N или ℕ - любое натуральное число (целое число от 1 до бесконечности)
- Z или ℤ - любое целое число (т. е. любое целое отрицательное, ноль, положительное)
- Q или ℚ - любое рациональное число (число, которое можно представить в виде обыкновенной дроби)
- R или ℝ - любое вещественное число (любое число, включая числа с десятичной точкой/запятой и знаками после запятой)
- C или ℂ - любое комплексное число (число с реальной и мнимой частью)
- H или
 - любой кватернион - любой кватернион
Ниже представлена большая таблица обозначений, принятых в русскоязычной среде. Следует учитывать, что в XXI веке многие математические школы перенимают манеру обозначений английских/американских научных заведений, и данная таблица не во всем применима к современным записям.
|
Знак (символ, сокращение) |
Пояснения (расшифровка, легенда) |
|
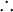
|
- следовательно,
- таким образом,
- поэтому
|
|
т.о. |
- следовательно,
- таким образом,
- поэтому
|
|

|
- потому что
- из-за того что
- вследствие того, что
- поскольку
- в результате того, что
|
|
ЧТД QED |
Конец доказательства = "Что и требовалось доказать" = quod erat demonstrandum |
|

|
Что и требовалось доказать = окончание доказательства |
|

|
Что и требовалось доказать = окончание доказательства |
|

|
Что и требовалось доказать = окончание доказательства |
|
= |
Равенство |
|

|
- приблизительно равно (везде)
|
|
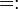
|
По определению равно |
|
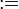
|
По определению равно |
|
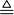
|
По определению равно |
|
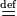
|
По определению равно |
|

|
По определению равно |
|

|
- По определению равно
- Равенство по модулю
Записывается a b (mod n), читается a равно b по модулю n. b (mod n), читается a равно b по модулю n. |
|
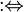
|
По определению логически эквивалентно |
|

|
- эквивалентность матриц (т.е. одна сводится к другой с помощью элементарных операций над строками)
- Случайная величина имеет распределение вероятности ...
- эквивалентность функций при определенной базе, т.е. одинаковое ассимптотическое поведение
- отношение эквивалентности , используется, когда 2 элемента принадлежат одному и тому же классу эквивалентности
|
|

|
- Конгруэнтность в геометрии
|
|
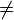
|
Неравенство |
|
< |
Меньше |
|
> |
Больше |
|
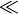
|
Много меньше |
|
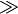
|
Много больше |
|
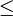 <= <=
|
Меньше или равно |
|
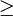 >= >=
|
Больше или равно |
|
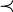
|
Сведение по Карпу (Karp reduction) - теория сложности, левое сводимо по Карпу к правому, левое "не сложнее правого", естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
|
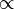
|
- пропорциональность - основной символ
- !иногда! сведение по Карпу (Karp reduction) - теория сложности, левое сводимо по Карпу к правому, левое "не сложнее правого", естественно возможно и использование знака острием вправо (но нам лень было рисовать)
|
|
+ |
- Несвязное объединение = несвязная сумма = дизъюнктное объединение - теория множеств
|
|
- |
- !иногда!Разность множеств - теория множеств
|
|
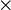
|
- Векторное произведение векторов
- Прямое (декартово) произведение множеств
- Группа единиц или группа обратимых элементов - теория колец: группа Rx - это обратимые элементы кольца R с той же опрецией умножения, что и на R. Так же обозначается как R* или U(R).
|
|
. |
- Скалярное произведение векторов в пространстве
- Производная по времени (записывается над аргументом)
|
|
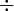
|
Разделить |
|
/ |
Если G -группа, а H- ее нормальная подгруппа, то G/H - факторгруппа G по H, т.е. группа классов смежности H в G
Если X - множество с заданным на нем отношением эквивалентности  , то X/ , то X/ - фактормножество, т.е. множество классов эквивалентности относительно - фактормножество, т.е. множество классов эквивалентности относительно  |
|
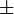
|
|
|
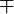
|
Минус плюс - имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) 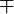 sin(x) sin(y). sin(x) sin(y). |
|
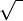
|
- Корень квадратный действительный
|
|
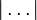
|
- Длина вектора (Евклидова норма)
- мощность множества (если оно бесконечно), количество элементов множества (порядок) (если оно конечно)
|
|
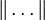
|
- Норма в нормированном векторном пространстве
- функция нахождения ближайшего целого числа (округления) (Другие варианты обозначения: [x], nint(x) или Round(x))
|
|
 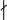
|
- не является делителем, не делит нацело
|
|
| |
- условная вероятность - в теории вероятностей
P(A|B) - вероятность события А, при условии, что событие B уже произошло
- ограничение функции на множестве, т.е. сужение области определения функции.
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f
- таких что......., так что..............
A={x | |x|<1} читается: "А - множество x таких, что модуль x меньше 1" и значит, что множество А - множество элементов числовой прямой, лежащих между -1 и 1. |
|
|| |
a||b - параллельные прямые a и b
- несравнимость (несравнимо) - в теории порядка
Если X - множество с отношением частичного порядка ≤, а a и b - его элементы, то a||b - a и b несравнимы, если про них невозможно сказать ни a≤b, ни b≤a
- точный делитель (при разложении числа в произведение степеней простых чисел - простое число в максимальной степени, делящее исходное)
|
|
# |
- мощность или кардинальное число в теории множеств
- связная сумма в топологии
n# - произведение простых чисел, не превышающих n |
|
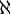
|
Алеф - кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
|
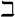
|
Бет - кардинальное число, характеризующее мощность бесконечного множества |
|

|
мощность континуума - теория множеств |
|
: |
- так что, такой что- везде
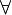 a a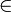 R R  b b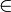 R : a<b - это читается как " для любого рационального числа a существует рациональное число b такое что a меньше b" R : a<b - это читается как " для любого рационального числа a существует рациональное число b такое что a меньше b"
- расширение поля - теория поля
E:K значит, что E - это расширение поля K
- скалярное произведение матриц в некотором предгильбертовом пространстве, элементами которого являются матрицы.
|
|
! |
n!=1*2*3.....*(n-1)*n читается n-факториал
!A=1, если А=0, !А=0, если А=1, читается не А. |
|

|
сплетение групп в теории групп (Также обозначается как АwrВ) |
|
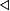
|
- инвариантная (нормальная) подгруппа
- Идеал кольца( теория колец )
|
|
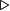
|
Антисоединение отношений (Antijoin) - операция реляционной алгебры, которая оставляет только те кортежи первого отношения, для которых не найдется кортежей второго отношения, совпадающих с ними по общему атрибуту. |
|
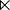
или
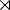
|
- Полупрямое произведение групп
- Полусоединение отношений (Semijoin)- операция реляционной алгебры, оставляющая только те кортежи первого отношения, для которых найдутся кортежи второго отношения, совпадающие с ними по общему атрибуту.
|
|
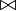
|
Естественное соединение отношений (Natural Join)- операция реляционной алгебры, результатом которой является набор всех возможных комбинаций кортежей исходных отношений, то есть комбинаций тех кортежей, у которых совпадают общие атрибуты |
|
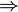
|
- Импликация (материальная), в логике
- Следовательно (в доказательствах)
|
|

|
- Импликация (материальная), в логике
- Стрелка, обозначающая откуда и куда действует отображение (функция) f. Запись f : X
 Y означает, что отображение f переводит элементы множества X в элементы множества Y. Или, можно сказать, что X - область определения f, а область значений f - есть некоторое подмножество множества Y. Y означает, что отображение f переводит элементы множества X в элементы множества Y. Или, можно сказать, что X - область определения f, а область значений f - есть некоторое подмножество множества Y.
- "Стремится" - в теории пределов
|
|

|
- импликация (материальная), в логике
- надмножество строгое (теория множеств) само понятие надмножества в русской традиции не вводится.
|
|

|
Материальная эквивалентность, равносильность= "тогда и только тогда" |
|

|
Материальная эквивалентность, равносильность= "тогда и только тогда" |
|

|
Логическое отрицание = не |
|

|
Логическое отрицание = не |
|
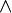
|
- Логическая конъюнкция (AND, И)
- Пересечение в теории графов
- V произведение - внешнее произведение - линейная алгебра
- Знак возведения в степень в строчной записи
|
|
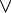
|
- Логическая дизъюнкция (OR, ИЛИ)
- Смыкание, сшивание в теории графов
|
|

|
- исключающее ИЛИ , симметрическая разность (логика, Булева алгебра, теория множеств)
- прямая сумма (абстрактая алгебра)
|
|
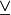
|
исключающее ИЛИ (только в логике) |
|
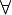
|
обозначение понятия - любой, читается как - "для любого", "для всех", "для каждого" |
|

|
обозначение понятия - существует, читается как "найдется", "существует", "существуют"... |
|

|
обозначение понятия - существует единственный, читается как "найдется ровно один ", "существует один и только один ", "существует единственный "... |
|
{ , } |
внутри скобок записываются элементы множества |
|
{ : } |
значок множества со значком определяющего признака элементов множеств. Читается, как элементы "икс", такие что "для всех икс верно....". |
|
{ | } |
значок множества со значком определяющего признака элементов множеств. Читается, как элементы "икс", такие что "для всех икс верно....". |
|
Ø |
значок пустого множества |
|
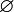
|
значок пустого множества |
|
{} |
значок пустого множества |
|
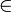
|
значок принадлежности к множеству - читается "принадлежит..." |
|
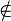
|
значок не принадлежности к множеству - читается "не принадлежит..." |
|

|
Знак подмножества. А  B означает - все элементы A являются элементами B. Часто путают со знаком ниже. B означает - все элементы A являются элементами B. Часто путают со знаком ниже. |
|

|
Знак собственного (строгого = истинного ) подмножества. А  B означает - все элементы A являются элементами B, но A не равно B. Часто путают со знаком выше. B означает - все элементы A являются элементами B, но A не равно B. Часто путают со знаком выше. |
|

|
Знак надмножества. А  B означает - все элементы B являются элементами A. В РФ очень часто вообще не используется (пользуются значком подмножества и переставляют буквы) B означает - все элементы B являются элементами A. В РФ очень часто вообще не используется (пользуются значком подмножества и переставляют буквы) |
|

|
Знак строгого = истинного надмножества. А  B означает - все элементы B являются элементами A, но B не равно A. В РФ очень часто вообще не используется (пользуются значком подмножества и переставляют буквы), кроме того этот знак путают со знаком выше. B означает - все элементы B являются элементами A, но B не равно A. В РФ очень часто вообще не используется (пользуются значком подмножества и переставляют буквы), кроме того этот знак путают со знаком выше. |
|
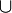
|
В теории множеств-объединение множеств. С= А 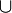 B означает, что элементы С - это элементы, принадлежащие хотя бы одному из множеств А и В. B означает, что элементы С - это элементы, принадлежащие хотя бы одному из множеств А и В. |
|

|
В теории множеств - пересечение множеств. С= А  B означает, что элементы множества С - это элементы, принадлежащие одновременно множествам А и В. B означает, что элементы множества С - это элементы, принадлежащие одновременно множествам А и В. |
|
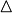
|
В теории множеств - симметрическая разность множеств. С= А 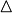 B значит, что элементами множества С являются элементы, принадлежащие только множеству А или только множеству В. B значит, что элементами множества С являются элементы, принадлежащие только множеству А или только множеству В. |
|
\ |
В теории множеств - разность множеств (или относительное дополнение одного множества до другого). С= А \ B читается С - разность множеств А и В (или С - относительное дополнение множества В до множества А) и значит, что элементами С являются все элементы А, которые не принадлежат В. |
|

|
Стрелка, определяющая отображение (функцию) f. Запись f: a  b означает, что отображение(функция) f переводит элемент а в элемент b. Наример, f: x b означает, что отображение(функция) f переводит элемент а в элемент b. Наример, f: x  x2 означает, что f(x)=x2 x2 означает, что f(x)=x2 |
|

|
- Композиция функций. Запись z=g
 f означает, что z(x)=g(f(x)). f означает, что z(x)=g(f(x)).
- Произведение Адамара двух матриц одинакового размера
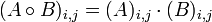 - матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц - матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц
|
|
 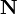
|
Множество натуральных чисел. В зависимости от контекста и области применения этого обозначения за  обозначают либо множество {1, 2, 3, 4, ...}, либо множество {0, 1, 2, 3, 4...}. обозначают либо множество {1, 2, 3, 4, ...}, либо множество {0, 1, 2, 3, 4...}. |
|
 
|
Множество целых чисел.  ={...-3, -2, -1, 0, 1, 2, 3, ...}. Также можно написать ={...-3, -2, -1, 0, 1, 2, 3, ...}. Также можно написать  ={p, -p| p∈ ={p, -p| p∈ } U {0}. } U {0}. |
|
 + +  > >
|
Множество положительных целых чисел. Т.е. множество {1, 2, 3, ...} |
|
 ≥ ≥
|
Множество неотрицательных целых чисел. Т.е. множество {0, 1, 2, ...} |
|
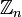 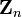
Z/(n)Z Z/(n) |
Кольцо вычетов по модулю n. 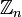 ={0, 1, 2,..., n-1} с операциями сложения и умножения по модулю n. Стоит понимать, что вместо n может стоять любая буква, а в частном случае цифра. ={0, 1, 2,..., n-1} с операциями сложения и умножения по модулю n. Стоит понимать, что вместо n может стоять любая буква, а в частном случае цифра. |
|
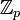 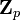
|
Множество p-адических чисел вида 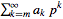 , где m≥0; ak - целые числа, а p - простое число. Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. , где m≥0; ak - целые числа, а p - простое число. Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|
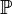 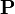
|
Проективное пространство. В частности, 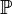 n- это n-мерное проективное пространство. n- это n-мерное проективное пространство. |
|
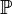 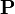 P(X) Pr(X) P[X] Pr[X] P(X) Pr(X) P[X] Pr[X]
|
В теории вероятности - вероятность. 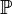 (X) - вероятность того, что произойдет событие X. (X) - вероятность того, что произойдет событие X. |
|
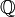 
|
Множество рациональных чисел. 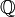 ={m/n | m∈ ={m/n | m∈ , n∈ , n∈ } } |
|
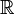 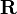
|
Множество действительных чисел |
|
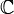 
|
Множество комплексных чисел. 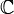 ={a+bi | a,b∈ ={a+bi | a,b∈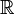 }, где i - мнимая единица. }, где i - мнимая единица. |
|
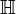 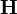
|
Множество кватернионов (кватернионов Гамильтона). 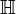 ={a+b i +c j +d k | a,b,c,d∈ ={a+b i +c j +d k | a,b,c,d∈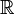 }, где { i, j, k } - стандартный базис трехмерного пространства. Другими словами, a - это рациональное число, а b i +c j +d k - это вектор трехмерного пространства с координатами {b, c, d}. }, где { i, j, k } - стандартный базис трехмерного пространства. Другими словами, a - это рациональное число, а b i +c j +d k - это вектор трехмерного пространства с координатами {b, c, d}. |
|
O |
O-большое в исследовании ассимптотического поведения функций. Описывает ассимптотическое поведение функции, когда ее аргумент стремится к числу или к бесконечности. Запись f(x)=O(g(x)) при x a означает, что lim f(x)/g(x)=K при x a означает, что lim f(x)/g(x)=K при x a. Где К - константа. a. Где К - константа. |
|
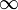
|
Бесконечность. Элемент расширенной числовой прямой, который больше любого числа. Чаще всего употребляется, когда речь идет о пределах. |
|
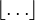
|
Огругление числа до целого в меньшую сторону.  x x - это наибольшее целое число, меньшее или равное х. Например, - это наибольшее целое число, меньшее или равное х. Например,  3.4 3.4 =3, =3,  -2, 3 -2, 3 = -3. = -3. |
|
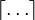
|
Огругление числа до целого в большую сторону.  x x -это наименьшее целое число, большее или равное х. Например, -это наименьшее целое число, большее или равное х. Например,  3.4 3.4 =4, =4,  -2.3 -2.3 =-2. =-2. |
|
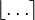
|
Огругление числа до ближайшего целого к нему. Например,  3.4 3.4 =3, =3,  -4.6 -4.6 =-5, =-5,  3.5 3.5 =4. =4. |
|
[ : ] |
- В теории полей - степень расширения поля. [E:K] - это степень расширения поля E:K, где E - это расширение поля K.
[E:K] - это по определению размерность векторного пространства E над K. Например, [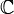 : : 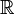 ]=2. ]=2.
- Индекс подгруппы Если H - подгруппа группы G, то [G:H] - индекс подгруппы H, т.е. число смежных классов по подгруппе H (или мощность множества смежных классов)
|
|
[ ] |
- Класс эквивалентности. [a] - это множество элементов, эквивалентных a. Более точная запись - [a]R означает класс эквивалентности, порожденный элементом a относительно отношения эквивалентности R.
- Огругление числа до целого в меньшую сторону. [x] - это наибольшее целое число, меньшее или равное х.
- Огругление числа до ближайшего целого к нему.
- Нотация Айверсона, или скобка Айверсона. Сопоставляет некоторому утверждению 1 или 0, в зависимости от того, истинно или ложно данное утверждение. Т.о., если S - некоторое утверждение, то [S]=0, если S - ложно, и [S]=1, если S - истинно.
Например, [2=3]=0; [4<5]=1.
- Если f - функция, а X - некоторое подмножество ее области определения, то f[X] - образ множества X.
Иными словами, f[X]={f(x) | x∈X} |
|
[ , ] |
- Отрезок. [a,b]={x∈
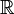 | a≤x≤b} | a≤x≤b}
- В алгебре - коммутатор.
[g, h] = g-1h-1gh, если g, h∈G, где G - группа. [a,b]=ab-ba, если a, b∈R, где R - кольцо. [A, B]=AB-BA, если A и B - операторы.
- Векторное произведение векторов.
|
|
[ , , ] |
Смешанное произведение векторов. |
|
( ) |
f(x) - образ x при применении f.
- Если f - функция, а X - некоторое подмножество ее области определения, то f(X) - образ множества X.
Иными словами, f(X)={f(x) | x∈X}
- Количество сочетаний. Например:

- число сочетаний из r элементов, выбранных из n элементов
- Скобки, указывающие порядок выполнения операций. Операция в скобках выполняется в первую очередь.
|
|
(( )) |
Количество мультимножеств. Например:
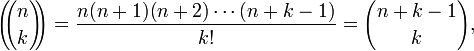
-число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
|
( , ) |
- Наибольший общий делитель.
(a, b)=НОД(a, b) - наибольший общий делитель чисел a и b.
- Кортеж - упорядоченный набор (список) некоторых величин, или горизонтальный вектор.
(a,b)={x∈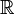 | a<x<b} | a<x<b}
- Скалярное произведение векторов
|
|
] , [ |
Интервал (a,b)={x∈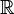 | a<x<b} | a<x<b} |
|
( , ] |
Полуинтервал (открытый слева) (a,b)={x∈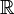 | a<x≤b} | a<x≤b} |
|
] , ] |
Полуинтервал (открытый слева) (a,b)={x∈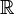 | a<x≤b} | a<x≤b} |
|
[ , ) |
Полуинтервал (открытый справа) (a,b)={x∈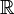 | a≤x<b} | a≤x<b} |
|
[ , [ |
Полуинтервал (открытый справа) (a,b)={x∈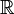 | a≤x<b} | a≤x<b} |
|
< > |
- Среднее значение, усреднение
<S> - среднее значение элементов множества S.
- В линейной алгебре - линейная оболочка подмножества линейного пространства - пересечение всех подпространств, содержащих данное подмножество.
Если S - подмножество линейного пространства L, <S> - линейная оболочка множества S, т.е. прересечение всех подпространств линейного пространства L, содержащих в себе множество S.
- В теории групп - группа, порожденная некоторым подмножеством элементов группы- минимальная подгруппа данной группы, содержащая в себе данное подмножество.
Если S - некоторое подмножество элементов группы G, то <S> - подгруппа G, порожденная S, т.е. минимальная подгруппа G, содержащая S. |
|
< , > |
- Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов)
- В линейной алгебре - линейная оболочка элементов линейного пространства- пересечение всех подпространств данного линейного пространства, содержащих данные элементы.
Если a1, a2...,an - векторы линейного пространства L, то <a1, a2...,an> - линейная оболочка векоторов a1, a2...,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2...,an.
- В теории групп - группа, порожденная данными элементами группы - минимальная подгруппа данной группы, содержащая в себе эти элементы.
Если a1, a2...,an- некоторые элементы группы G, то <a1, a2...,an> - подгруппа G, порожденная элементами a1, a2...,an, т.е. минимальная подгруппа G, содержащая в себе элементы a1, a2...,an.
- Кортеж - упорядоченный набор (список) некоторых величин, или горизонтальный вектор.
|
|
< | > |
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) |
|
( | ) |
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) |
|
| > |
В обозначениях Дирака - кет-вектор. |φ> - вектор φ некоторого гильбертого пространства |
|
< | |
В обозначениях Дирака - бра-вектор из пространства, сопряженного некоторому гильбертовому пространству. <φ| - бра вектор, соответствующий кет-вектору |φ> (говорят, даже, совпадающий с кет-фектором |φ>), задающий линейный функционал, ставящий в соответствие каждому кет-вектору |ψ> скалярное произведение <φ|ψ>. |
|
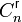
|
число сочетаний из r элементов, выбранных из n элементов |
|

|
Сумма, ряд.
|
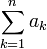
|
=a1+...+an |
|
| |
|

|
|
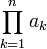
|
=a1...an |
|
|
- В теории множеств - прямое (декартово) произведение множеств
|
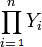
|
- множество n-местных кортежей (наборов), в которых на i-м месте стоит элемент из Yi. |
|
| |
|

|
В теории категорий - копроизведение (категорная сумма) |
|

|
Производная. f'(x) - значение производной функции f в точке x (Тангенс угла наклона касательно к функции f в точке x). |
|
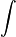
|
- Неопределенный интеграл (первообразная)
|
A(x)= |
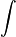
|
f(x)dx значит, что A'(x)=f(x). |
|
|
|
|
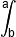
|
f(x)dx |
- |
площадь (с учетом знака) фигуры, образованной графиком функции f(x)dx, прямой Ox и прямыми x=a и x=b. |
|
|
|
|
- Криволинейный интеграл по незамкнутой кривой (первого или второго рода).
|
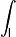
|
f(x,y,z)dl |
- |
криволинейный интеграл первого рода функции f по кривой l. |
|
|
|
|
|
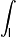
|
f(x,y,z)dx |
- |
криволинейный интеграл второго рода функции f по кривой l. |
|
|
|
|
|
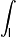
|
f(x,y,z)dy |
- |
криволинейный интеграл второго рода функции f по кривой l. |
|
|
|
|
|
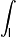
|
f(x,y,z)dz |
- |
криволинейный интеграл второго рода функции f по кривой l. |
|
|
|
| |
|
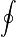
|
Интеграл по контуру (по поверхности - знак интеграла удваивается, по объему-знак интеграла утраивается). |
|
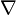
|
- Градиент
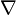 f(x1,...,xn)- вектор частных производных (f 'x1,..,f 'xn) f(x1,...,xn)- вектор частных производных (f 'x1,..,f 'xn)
Если вектор 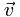 =vx i +vy j +vz k , где vx, vy, vz - функции от трех переменных x, y, z, а i, j, k - стандартный базис в пространстве, то =vx i +vy j +vz k , где vx, vy, vz - функции от трех переменных x, y, z, а i, j, k - стандартный базис в пространстве, то
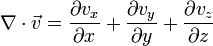
Если вектор 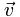 =vx i +vy j +vz k , =vx i +vy j +vz k ,
где vx, vy, vz - функции от трех переменных x, y, z, а i, j, k - стандартный базис в пространстве, то
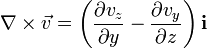
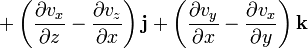
|
|
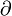
|
|
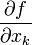
|
- |
частная производная функции f по переменной xk, где f = f(x1,..,xk,..,xn) |
- В топологии - граница множества
Если M - некоторое множество, то 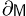 - граница множества M (другими словами, множество всех граничных точек множества M) - граница множества M (другими словами, множество всех граничных точек множества M)
Если f - многочлен, то 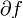 - степень многочлена f. Чаще встречается обозначение deg f. - степень многочлена f. Чаще встречается обозначение deg f. |
|
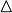
|
- Приращение , дельта,
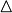 x - приращение (изменение) x x - приращение (изменение) x
Оператор Лапласа ставит функции от n переменных в соответствие ее дифференциал второго порядка.
- Определитель матрицы
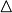 (А), где А - матрица (А), где А - матрица
|
|
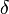
|
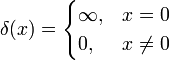
- Символ Кронекера, индикатор равенства переменных
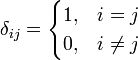
|
|
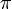
|
- В реляционной алгебре - проекция
Операция, которая из заданного отношения (таблицы) выбирает подмножество, которое получается выбором нескольких из имеющихся атрибутов и (если потребуется) вычеркиванием повторяющихся кортежей. Результатом перации 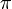 a,b,..,k(R) является таблица (отношение), полученная из таблицы R вычеркиванием атрибутов, не равных a,b,...k, и затем вычеркиванием одинаковых строчек (кортежей), если такие появились. Например: Если в изначальной таблице ЛЮДИ атрибутами являются рост, вес, пол, то результатом операции a,b,..,k(R) является таблица (отношение), полученная из таблицы R вычеркиванием атрибутов, не равных a,b,...k, и затем вычеркиванием одинаковых строчек (кортежей), если такие появились. Например: Если в изначальной таблице ЛЮДИ атрибутами являются рост, вес, пол, то результатом операции 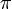 рост(ЛЮДИ) будет таблица ЛЮДИ с одним атрибутом - рост, и если в ней окажутся одигнаковые строки, они будут вычеркнуты. рост(ЛЮДИ) будет таблица ЛЮДИ с одним атрибутом - рост, и если в ней окажутся одигнаковые строки, они будут вычеркнуты.
Математическая константа, равная отношению длины окружности к ее диаметру. 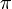  3,14159265. 3,14159265. |
|
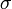
|
В реляционной алгебре - выборка Операция 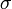 aθb(v)(R), где a и b - атрибуты (или a-атрибут, а v -константа), а θ - бинарная операция из множества {<, ≤, =, ≥, >} выбирает из отношения R те кортежи, для атрибутов которых выполнено соотношение aθb (aθv). aθb(v)(R), где a и b - атрибуты (или a-атрибут, а v -константа), а θ - бинарная операция из множества {<, ≤, =, ≥, >} выбирает из отношения R те кортежи, для атрибутов которых выполнено соотношение aθb (aθv). |
|
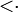
|
В теории порядка - покрытие (понятие, определяющее смежность вершин диаграммы Хассе некоторого частично-упорядоченного множества). Если X - множество с отношением частичного порядка ≤ , а отношение < на этом множестве задается следующим образом : a<b, если a≤b и а ≠ b, то элемент y покрывает элемент x и пишется x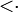 y, если а) x<y y, если а) x<y
б) не существует такого элемента z, что
x<z<y. Если a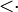 b, то вершины a и b диаграммы Хассе данного множества смежные. b, то вершины a и b диаграммы Хассе данного множества смежные. |
|

|
В теории типов - подтип (подкласс, дочерний тип(класс)). Часто используется в объектно-ориентированном программировании.
S T значит, что S - подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. T значит, что S - подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство.
Например, Круги Фигуры. Фигуры.
S T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. |
|
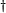
|
Эрмитово-сопряженная (комплексно-сопряженная) матрица. A† - матрица, полученная из матрицы A транспонированием и заменой каждого элемента матрицы A комплексно-сопряженным ему. Чаще всего такая матрица обозначается A*, а также встречаются обозначения A*T, AT*, 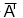 , , 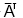 . . |
|

|
Транспонирование матрицы. AT - матрица, в которой в качестве строк записаны столбцы матрицы А.
Другими словами, если А=(aij), то AT=(aji) |
|
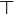
|
- Наибольший элемент решетки - в теории порядка
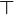 - наибольший (верхний )элемент решетки. - наибольший (верхний )элемент решетки.
- Высший (универсальный) тип в теории типов.
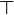 - тип, который содержит в себе каждый возможный объект в данной системе типов. - тип, который содержит в себе каждый возможный объект в данной системе типов.
|
|
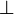
|
- Перпендикуляр - в геометрии
x⊥y значит, что векторы (прямые) x и y перпендикулярны, или, в более общем случае, ортогональны.
- Ортогональное дополнение подпространства - в линейной алгебре
Если W - подпространство предгильбертового пространства V, то W⊥ - ортогональное дополнение подпространства W, т.е. множество векторов пространства V, перпендикулярных каждому из векторов подпространства W.
- Взаимно простые числа - в теории чисел
a⊥b значит, что наибольший общий делитель чисел a и b равен единице. Часто записывается как (a, b)=1
- Независимость случайных событий - в теории вероятностей
A⊥B значит, что случайные события A и B независимы, т.е. наступление одного из них не влияет на вероятность наступления другого.
- Наименьший (нижний) элемент решетки - в теории порядка
⊥ - наименьший (нижний) элемент решетки
- Нижайший тип (универсальный подтип) - в теории типов
⊥ - тип, у которого нет подтипов
- Сравнимость - в теории порядка
x⊥y значит, что элементы x и y частично упорядоченного множества сравнимы, т.е. про них известно, что x≤y или y≤x |
|

|
Импликация (логическое следование) - в теории моделей A  B значит, что из А следует B, или A влечет B. В любой модели, где A B значит, что из А следует B, или A влечет B. В любой модели, где A  B, если А верно, то и B верно. B, если А верно, то и B верно. |
|
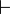
|
Вывод - в логике высказываний (предикатов). A 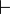 B значит, что B выводится из A. B значит, что B выводится из A. |
|
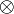
|
Тензорное произведение (модулей) - в линейной алгебре. Если A и B - линейные пространства, то
A 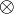 B - их тензорное произведение, тоже линейное пространство Если а B - их тензорное произведение, тоже линейное пространство Если а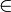 A и b A и b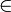 B, то B, то
a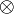 b - их тензорное произведение, и b - их тензорное произведение, и
Если A и B - модули над коммутативным кольцом R, то A 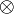 R B - их тензорное произведение, тоже модуль над кольцом R R B - их тензорное произведение, тоже модуль над кольцом R |
|

|
a b - произведение a и b b - произведение a и b
- Свертка функций - в функциональном анализе
|
(f*g)(x) = |
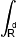
|
f(y)g(x-y)dy, |
где f, g - функции, определенные и интегрируемые относительно меры Лебега на пространстве Rd
- Сопряжение комплексных чисел
z* - число, комплексно-сопряженное к z.
Если z=a+bi, то z*=a-bi
- Группа единиц (обратимых элементов) кольца
R* - группа обратимых элементов кольца R
- Гипердействительные числа
R* - расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа.
Вместо R можно использовать также другие множества, например, N*.
Линейный оператор из пространства p-векторов в пространства (n-p)-форм. Если вектор v - поливектор степени p, то *v - дифференциальная форма степени n-p. |
|
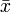
|
- Среднее значение - в статистике
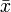 - среднее значение величин xi - среднее значение величин xi
- Сопряжение комплексных чисел
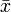 - число, комплексно-сопряженное к x. Если x=a+bi, то - число, комплексно-сопряженное к x. Если x=a+bi, то 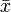 =a-bi =a-bi
- Алгебраическое замыкание - в алгебре
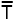 - алгебраическое замыкание поля T, т.е. алгебраически замкнутое расширение поля T. Поле называется алгебраически замкнутым, если каждый многочлен ненулевой степени над этим полем имеет хотя бы 1 корень. - алгебраическое замыкание поля T, т.е. алгебраически замкнутое расширение поля T. Поле называется алгебраически замкнутым, если каждый многочлен ненулевой степени над этим полем имеет хотя бы 1 корень.
- Топологическое замыкание - в геометрии (топологии)
Если S - некоторое подмножество топологического пространства, то 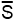 - топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S. - топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S. |
|


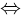 - обозначает равносильность. Например,
- обозначает равносильность. Например, 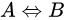 следует читать
следует читать - любой кватернион
- любой кватернион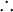





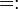
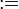
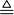
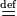



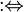


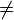
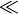
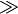
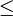
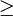
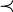
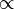
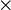
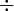



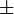
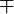
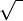
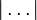
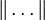

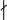
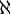
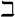

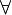 a
a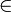 R
R  b
b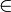 R : a<b - это читается как " для любого рационального числа a существует рациональное число b такое что a меньше b"
R : a<b - это читается как " для любого рационального числа a существует рациональное число b такое что a меньше b" 
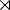
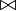
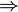

 Y означает, что отображение f переводит элементы множества X в элементы множества Y. Или, можно сказать, что X - область определения f, а область значений f - есть некоторое подмножество множества Y.
Y означает, что отображение f переводит элементы множества X в элементы множества Y. Или, можно сказать, что X - область определения f, а область значений f - есть некоторое подмножество множества Y.




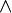
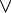

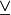
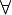


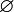
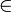
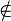







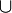
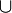


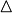


 f означает, что z(x)=g(f(x)).
f означает, что z(x)=g(f(x)). 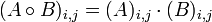

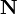








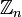
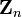
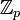
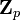
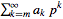
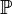
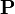
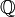

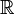
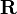
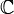

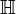
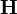


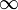
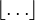






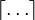






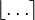






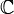
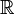
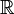 | a≤x≤b}
| a≤x≤b} 
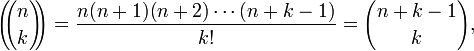
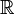
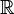
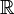
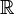
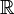
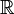
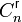

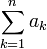

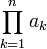
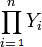


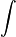
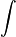
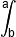
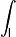
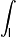
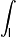
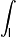
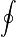
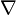
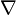 f(x
f(x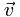
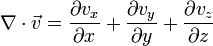
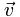
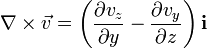
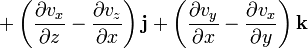
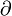
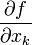
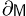
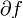
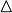
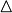 x - приращение (изменение) x
x - приращение (изменение) x 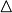 (А), где А - матрица
(А), где А - матрица