Данная статья не стремится к научной полноте и не содержит формул, однако включает ссылки на исследования, которые были использованы при её подготовке. Статья призвана познакомить читателя с тем, как биологические механизмы могут применяться при разработке искусственных нейронных сетей для создания сильного искусственного интеллекта (AGI).

В прошлой статье [1] мы рассмотрели сложную структуру нейронной сети в виде кортикальных колонок. Однако передача сигнала в ней осталась такой же, как в обычных искусственных нейронных сетях. Давайте заменим её на биологический вариант.

В традиционных сетях сигнал передаётся непрерывно: нейрон сразу выдаёт число, которое передаётся дальше по сети. Нейроны в слоях обычно работают синхронно — все одновременно вычисляют своё значение и передают его следующему слою.

Биологические нейроны устроены иначе. Они не передают непрерывные числа, а генерируют короткие электрические импульсы, называемые спайками. Спайк — это дискретное событие: либо нейрон «выстрелил», либо нет. Информация кодируется не в амплитуде сигнала, а в частоте и точном времени спайков [2].

Мозг анализирует паттерны этих импульсов: когда именно и как часто нейрон «щелкает». При этом нейроны в мозге работают асинхронно — каждый может активироваться в своё время, независимо от соседей.

Один нейрон может генерировать 3 спайка в секунду, другой — 10, и мозг извлекает информацию именно из этих паттернов активности. Таким образом, кодирование информации происходит не только через то, какие нейроны активны, но и через ритм их импульсов.

Один из популярных типов спайковых нейронов называется «нейрон с утечкой» (Leaky Integrate-and-Fire, LIF). Он имитирует мембранный потенциал биологического нейрона: потенциал накапливается при получении входных спайков и постепенно «утекает» со временем. Когда потенциал достигает порогового значения, нейрон генерирует выходной спайк и сбрасывается к исходному уровню [2].

Создадим новый файл под названием brain_spiking.py и импортируем необходимые пакеты:

#!/usr/bin/env python3

import torch

from torch import nn

import torch.nn.functional as F

import networkx as nx

import math

Для создания LIF-нейрона нам понадобится указать его свойства:

• tau_mem — «время утечки» мембранного потенциала. Чем больше, тем дольше нейрон «помнит» прошлые входные сигналы.
• tau_syn — «время утечки» синаптического тока. Определяет, как быстро текущий входной сигнал затухает.
• threshold — порог, при котором нейрон спайкает, отправляя сигнал дальше.
• reset — значение мембранного потенциала после спайка.

class LIFNeuron(nn.Module):

def __init__(self, tau_mem: float = 20.0, tau_syn: float = 5.0, threshold: float = 2.0, reset: float = 0.0):

super().__init__()

self.threshold = threshold

self.reset = reset

self.register_buffer('alpha', torch.tensor(math.exp(-1.0 / tau_mem)))

self.register_buffer('beta', torch.tensor(math.exp(-1.0 / tau_syn)))

def forward(self, input_current, mem, syn):

syn = self.beta * syn + input_current

mem = self.alpha * mem + syn

spike = (mem >= self.threshold).float()

mem = mem * (1.0 - spike) + self.reset * spike

return spike, mem, syn

Механизм работы нейрона следующий: входные сигналы input_current от других нейронов формируют синаптический ток syn, который влияет на мембранный потенциал mem. Если накопленный потенциал превышает пороговое значение, нейрон генерирует спайк и возвращает мембрану к начальному состоянию self.reset. При недостаточном входном токе мембранный потенциал постепенно уменьшается с коэффициентом затухания self.alpha.

По аналогии с предыдущей статьей создадим класс кортикальной колонки, но заменим обычные нейроны на спайковые LIF-нейроны. На вход колонки поставим линейные слои для преобразования входных спайков в токи для каждого LIF-нейрона. Эти токи затем передаются в слои возбуждающих и тормозящих LIF-нейронов в соотношении 80% возбуждающих и 20% тормозящих [3]. Для каждого типа нейронов зададим разные пороги и времена утечки. Инициализируем входные слои методом Каминга с учётом нелинейности ReLU, для стабилизации дисперсии сигналов:

class SpikeColumn(nn.Module):

def __init__(self, in_feat: int, out_feat: int, e_i_ratio: float = 0.8, tau_mem: float = 20.0, tau_syn: float = 5.0):

super().__init__()

self.out_feat = out_feat

self.n_exc = int(out_feat * e_i_ratio)

self.n_inh = out_feat - self.n_exc

self.fc_exc = nn.Linear(in_feat, self.n_exc, bias=False)

self.fc_inh = nn.Linear(in_feat, self.n_inh, bias=False)

self.lif_exc = LIFNeuron(tau_mem=tau_mem, tau_syn=tau_syn, threshold=2.5)

self.lif_inh = LIFNeuron(tau_mem=tau_mem*0.8, tau_syn=tau_syn*0.8, threshold=2.0)

nn.init.kaiming_normal_(self.fc_exc.weight, nonlinearity='relu')

nn.init.kaiming_normal_(self.fc_inh.weight, nonlinearity='relu')

with torch.no_grad():

self.fc_exc.weight *= 0.3

self.fc_inh.weight *= -0.3

def init_state(self, batch_size, device):

return {

'mem_exc': torch.zeros(batch_size, self.n_exc, device=device),

'syn_exc': torch.zeros(batch_size, self.n_exc, device=device),

'mem_inh': torch.zeros(batch_size, self.n_inh, device=device),

'syn_inh': torch.zeros(batch_size, self.n_inh, device=device),

}

def forward(self, spike_input, state):

current_exc = self.fc_exc(spike_input)

current_inh = self.fc_inh(spike_input)

spike_exc, mem_exc, syn_exc = self.lif_exc(current_exc, state['mem_exc'], state['syn_exc'])

spike_inh, mem_inh, syn_inh = self.lif_inh(current_inh, state['mem_inh'], state['syn_inh'])

spikes = torch.cat([spike_exc, -spike_inh], dim=1)

new_state = {

'mem_exc': mem_exc,

'syn_exc': syn_exc,

'mem_inh': mem_inh,

'syn_inh': syn_inh,

}

return spikes, new_state

При работе (метод forward) наша спайковая кортикальная колонка преобразует входные спайки в токи, которые затем обрабатываются LIF-нейронами для генерации выходных спайков.

Теперь, для сохранения сложной топологии межколоночных связей, добавим вспомогательную функцию создания графа «малого мира» из предыдущей статьи:

def make_small_world(num_nodes: int, k: int = 4, p: float = 0.1) -> torch.Tensor:

G = nx.watts_strogatz_graph(num_nodes, k, p)

adj = torch.zeros(num_nodes, num_nodes, dtype=torch.float32)

for i, j in G.edges():

adj[i, j] = 1.0

adj[j, i] = 1.0

return adj

Биологические нейронные сети не просто передают спайки — они обладают синаптической пластичностью: если две структуры часто активируются вместе, их связь усиливается; если редко — ослабевает. В нашей архитектуре топология «малого мира» определяет возможные связи между колонками. Добавим механизм STDP (Spike-Timing-Dependent Plasticity), который будет динамически регулировать силу этих межколоночных связей на основе совместной активности колонок:

class STDP(nn.Module):

def __init__(self, num_columns: int, tau_plus: float = 20.0, tau_minus: float = 20.0, a_plus: float = 0.01, a_minus: float = 0.012, formation_threshold: float = 0.8, pruning_threshold: float = 0.05, max_density: float = 0.25):

super().__init__()

self.num_columns = num_columns

self.a_plus = a_plus

self.a_minus = a_minus

self.formation_threshold = formation_threshold

self.pruning_threshold = pruning_threshold

self.max_density = max_density

self.register_buffer('decay_plus', torch.tensor(math.exp(-1.0 / tau_plus)))

self.register_buffer('decay_minus', torch.tensor(math.exp(-1.0 / tau_minus)))

self.register_buffer('connection_potential', torch.zeros(num_columns, num_columns))

self.register_buffer('connection_usage', torch.zeros(num_columns, num_columns))

def compute_update(self, pre_spikes, post_spikes, pre_trace, post_trace):

pre_trace = self.decay_plus * pre_trace + pre_spikes

post_trace = self.decay_minus * post_trace + post_spikes

ltp = self.a_plus * torch.ger(post_spikes, pre_trace)

ltd = -self.a_minus * torch.ger(post_trace, pre_spikes)

return ltp + ltd, pre_trace, post_trace

def update_connection_potential(self, pre_activity, post_activity):

correlation = torch.ger(post_activity, pre_activity)

self.connection_potential = 0.99 * self.connection_potential + 0.01 * correlation

def update_connection_usage(self, adjacency_mask, weight_strength):

usage = adjacency_mask * weight_strength.abs()

self.connection_usage = 0.95 * self.connection_usage + 0.05 * usage

Важно понимать: STDP в данной реализации работает на уровне колонок, а не отдельных нейронов. Это сделано для возможности расчетов на обычном оборудовании (CPU или GPU), в противном случае, при включении STDP на уровне нейронов понадобится специализированный нейроморфный процессор, позволяющий нейронам спайкать на аппаратном уровне [4]. Данный код также может быть преобразован в нейроморфный вариант [5] для выполнения на нейроморфном железе, однако недоступность подобных процессоров выводит эту тему за рамки статьи.

Параметры pre_spikes и post_spikes представляют собой агрегированную активность колонок (усреднённую частоту спайков всех нейронов в колонке)[6]. Механизм отслеживает, какие пары колонок часто активируются вместе, и соответствующим образом модифицирует веса связей между ними.

Механизм работы STDP включает два ключевых процесса:

• Long-Term Potentiation (LTP) — усиление связи, когда постсинаптическая колонка активируется вскоре после пресинаптической
• Long-Term Depression (LTD) — ослабление связи при обратном порядке активации

Дополнительно отслеживаются два показателя:

• connection_potential — потенциал формирования новых связей между колонками на основе их корреляции
• connection_usage — активность использования существующих связей

Мы описали все необходимые элементы и теперь можем создать кортикально-спайковую нейронную сеть с полной динамической топологией на уровне кортикальных колонок:

class DynamicTopologyNetwork(nn.Module):

def __init__(self,

num_columns: int = 64,

in_dim: int = 784,

col_out: int = 128,

top_out: int = 10,

graph_k: int = 8,

graph_p: float = 0.15,

time_steps: int = 50,

e_i_ratio: float = 0.8,

tau_mem: float = 20.0,

tau_syn: float = 5.0,

use_dynamic_topology: bool = True,

topology_update_freq: int = 100,

stdp_lr: float = 5e-5):

super().__init__()

self.num_columns = num_columns

self.time_steps = time_steps

self.col_out = col_out

self.use_dynamic_topology = use_dynamic_topology

self.topology_update_freq = topology_update_freq

self.stdp_lr = stdp_lr

self.register_buffer('training_step', torch.tensor(0))

self.input_scale = nn.Parameter(torch.ones(in_dim) * 0.5)

self.columns = nn.ModuleList([SpikeColumn(in_dim, col_out, e_i_ratio=e_i_ratio, tau_mem=tau_mem, tau_syn=tau_syn) for _ in range(num_columns)])

initial_topology = make_small_world(num_columns, k=graph_k, p=graph_p)

if use_dynamic_topology:

self.topology = nn.Parameter(initial_topology, requires_grad=False)

else:

self.register_buffer('topology', initial_topology)

self.inter_weights = nn.Parameter(torch.randn(num_columns, num_columns) * 0.05)

self.stdp = STDP(num_columns)

self.register_buffer('pre_trace', torch.zeros(num_columns))

self.register_buffer('post_trace', torch.zeros(num_columns))

self.readout = nn.Sequential(

nn.Linear(num_columns * col_out, 512),

nn.ReLU(),

nn.Dropout(0.2),

nn.Linear(512, top_out)

)

self.register_buffer('spike_rate_avg', torch.ones(num_columns) * 0.05)

self.register_buffer('target_rate', torch.tensor(0.05))

def _update_topology(self):

with torch.no_grad():

current_density = self.topology.sum().item() / (self.num_columns ** 2)

no_connection = (self.topology.data == 0)

high_potential = (self.stdp.connection_potential > self.stdp.formation_threshold)

candidates_for_formation = no_connection & high_potential

if current_density < self.stdp.max_density:

num_to_add = int((self.stdp.max_density - current_density) * self.num_columns ** 2)

if num_to_add > 0 and candidates_for_formation.sum() > 0:

potential_flat = self.stdp.connection_potential[candidates_for_formation]

if len(potential_flat) > num_to_add:

threshold = torch.topk(potential_flat, num_to_add).values[-1]

to_add = candidates_for_formation & (self.stdp.connection_potential >= threshold)

else:

to_add = candidates_for_formation

self.topology.data[to_add] = 1.0

num_added = to_add.sum().item()

has_connection = (self.topology.data > 0)

low_usage = (self.stdp.connection_usage < self.stdp.pruning_threshold)

weak_weights = (self.inter_weights.data.abs() < 0.1)

candidates_for_pruning = has_connection & low_usage & weak_weights

num_to_remove = candidates_for_pruning.sum().item()

if num_to_remove > 0:

self.topology.data[candidates_for_pruning] = 0.0

self.inter_weights.data[candidates_for_pruning] = 0.0

def _poisson_encode(self, x, deterministic=False):

x_scaled = torch.sigmoid(x * self.input_scale) * 0.5

if deterministic:

k = int(x.shape[1] * 0.1)

topk_vals, topk_idx = torch.topk(x_scaled, k, dim=1)

spikes = torch.zeros_like(x_scaled)

spikes.scatter_(1, topk_idx, (topk_vals > 0.3).float())

else:

spikes = (torch.rand_like(x_scaled) < x_scaled).float()

return spikes

def forward(self, x, learn=None):

if learn is None:

learn = self.training

batch_size = x.shape[0]

device = x.device

column_states = [col.init_state(batch_size, device) for col in self.columns]

spike_accumulator = torch.zeros(batch_size, self.num_columns, self.col_out, device=device)

inter_weights = torch.sigmoid(self.inter_weights) * self.topology

if learn:

pre_spikes_history = []

post_spikes_history = []

for t in range(self.time_steps):

input_spikes = self._poisson_encode(x, deterministic=not self.training)

current_column_spikes = []

for col_idx, column in enumerate(self.columns):

spikes, new_state = column(input_spikes, column_states[col_idx])

column_states[col_idx] = new_state

current_column_spikes.append(spikes)

all_spikes = torch.stack(current_column_spikes, dim=1)

col_spike_rates = all_spikes.mean(dim=2)

inter_influence = torch.matmul(col_spike_rates, inter_weights.t())

modulated_spikes = all_spikes * (1.0 + 0.1 * inter_influence.unsqueeze(-1))

spike_accumulator += modulated_spikes

if learn and t > 0:

pre_spikes_history.append(col_spike_rates.mean(dim=0).detach())

post_spikes_history.append(col_spike_rates.mean(dim=0).detach())

if learn and len(pre_spikes_history) > 1:

with torch.no_grad():

current_avg_rate = spike_accumulator.abs().mean() / self.time_steps

adaptive_lr = self.stdp_lr * (self.target_rate / (current_avg_rate + 1e-6)).clamp(0.5, 2.0)

for i in range(0, len(pre_spikes_history) - 1, 10):

pre = pre_spikes_history[i]

post = post_spikes_history[i + 1]

self.stdp.update_connection_potential(pre, post)

self.stdp.update_connection_usage(self.topology, self.inter_weights)

delta, self.pre_trace, self.post_trace = self.stdp.compute_update(

pre, post, self.pre_trace, self.post_trace

)

delta = delta * self.topology

self.inter_weights.data += adaptive_lr * delta

self.inter_weights.data.clamp_(-2.0, 2.0)

if self.use_dynamic_topology:

self.training_step += 1

if self.training_step % self.topology_update_freq == 0:

self._update_topology()

spike_rates = spike_accumulator / self.time_steps

with torch.no_grad():

current_rates = spike_rates.abs().mean(dim=(0, 2))

self.spike_rate_avg = 0.95 * self.spike_rate_avg + 0.05 * current_rates

if self.training:

mean_rate = current_rates.mean()

if mean_rate < 0.03:

self.target_rate = torch.clamp(self.target_rate * 1.1, 0.03, 0.08)

elif mean_rate > 0.08:

self.target_rate = torch.clamp(self.target_rate * 0.9, 0.03, 0.08)

scale = torch.clamp(self.target_rate / (self.spike_rate_avg.unsqueeze(-1) + 1e-6), 0.3, 3.0)

spike_rates = spike_rates * scale.unsqueeze(0)

features = spike_rates.reshape(batch_size, -1)

logits = self.readout(features)

return logits, current_rates

Это не просто спайковая нейронная сеть (SNN) — это самоорганизующаяся система с динамически изменяющейся топологией. Связи между колонками могут формироваться (когда колонки часто активируются совместно) и исчезать (когда связь слабо используется), создавая адаптивную архитектуру, более близкую к биологическим нейронным сетям [7]. STDP модифицирует только те веса, где small world топология разрешает связь.

Архитектура работает на двух различных уровнях организации, каждый со своими механизмами и принципами:

1. Внутри колонки: локальная спайковая динамика

На уровне отдельной колонки происходит обработка входных сигналов через спайковые механизмы:

• LIF-нейроны — основные вычислительные элементы. Каждая колонка содержит популяцию возбуждающих (80%) и тормозящих (20%) нейронов, которые работают параллельно и асинхронно.
• Мембранный потенциал — это «внутреннее состояние» каждого нейрона. Он накапливается при получении входных токов и постепенно утекает со временем (константа tau_mem). Когда потенциал достигает порога, нейрон генерирует спайк и сбрасывается.
• Спайки — дискретные события активации нейронов. Информация кодируется не амплитудой, а частотой и точным временем спайков. Нейрон может генерировать 3, 10 или 50 спайков в течение временного окна — это и есть его ответ на входной паттерн.
• Локальная динамика — взаимодействие возбуждающих и тормозящих нейронов внутри колонки создаёт сложные паттерны активности. Тормозящие нейроны регулируют общий уровень возбуждения, предотвращая перенасыщение и создавая ритмические колебания.
2. Между колонками: адаптивная топология

На уровне межколоночных взаимодействий происходит самоорганизация структуры сети:

• STDP (Spike-Timing-Dependent Plasticity) — механизм пластичности, который отслеживает совместную активность пар колонок. Если колонка B активируется вскоре после колонки A, их связь усиливается (LTP). Если порядок обратный — связь ослабляется (LTD).
• Корреляции активности — STDP вычисляет connection_potential между всеми парами колонок, измеряя, насколько часто они активируются вместе. Высокий потенциал указывает на функциональную связь, даже если физическое соединение ещё не существует.
• Формирование связей — если две колонки демонстрируют устойчиво высокий connection_potential (выше порога formation_threshold), между ними может быть создана новая связь. Это позволяет сети адаптировать свою структуру под обрабатываемые данные.
• Удаление связей (pruning) — слабо используемые связи с низким connection_usage и малыми весами удаляются. Это предотвращает переусложнение сети и освобождает ресурсы для более важных соединений.
• Изменение структуры сети — процедура _update_topology() периодически (каждые topology_update_freq шагов) пересматривает граф связей: добавляет перспективные соединения и удаляет неэффективные. Сеть буквально «перестраивает сама себя» в процессе обучения.

Таким образом, внутри колонок происходит быстрая спайковая обработка на временных масштабах миллисекунд, а между колонками — медленная структурная адаптация на масштабах сотен обучающих итераций. Эти два уровня работают согласованно, создавая гибкую и адаптивную архитектуру.

Теперь протестируем архитектуру на практике. Создадим файл train_spiking_brain.py для обучения сети на датасете MNIST. Мы намеренно используем тот же датасет, что и в предыдущей статье, чтобы продемонстрировать эволюцию подхода на знакомой задаче.

Цель эксперимента — не превзойти традиционные нейросети по метрикам точности, а показать, что гибридная архитектура, сочетающая биологические принципы со элементами искусственных сетей, достигает сопоставимых результатов, одновременно открывая значительно более богатое пространство для представления и обработки информации [8]. Код обучения довольно простой, поэтому обойдемся комментариями прямо в коде:

#!/usr/bin/env python3

import torch

import torch.nn.functional as F

from torchvision import datasets, transforms

from torch.utils.data import DataLoader

from brain_spiking import DynamicTopologyNetwork

import time

batch_size = 128 # размер батча для обучения

epochs = 40 # количество полных проходов по датасету

learning_rate = 5e-4 # скорость обучения для градиентного спуска

weight_decay = 1e-4 # L2-регуляризация для предотвращения переобучения

hyperparams = {

"num_columns": 64, # количество кортикальных колонок в сети

"in_dim": 784, # размерность входа (28×28 пикселей MNIST)

"col_out": 128, # количество нейронов (возб.+торм.) в каждой колонке

"top_out": 10, # количество выходных классов (цифры 0-9)

"graph_k": 8, # количество ближайших соседей в топологии малого мира

"graph_p": 0.15, # вероятность дальних связей в графе малого мира

"time_steps": 50, # количество временных шагов для развёртки спайковой динамики

"e_i_ratio": 0.8, # доля возбуждающих нейронов

"tau_mem": 20.0, # константа времени утечки мембранного потенциала (больше = дольше память)

"tau_syn": 5.0, # константа времени утечки синаптического тока (скорость затухания входа)

"use_dynamic_topology": True, # разрешить рост и удаление связей между колонками

"topology_update_freq": 100, # частота пересмотра топологии (каждые N шагов обучения)

"stdp_lr": 5e-5 # скорость пластичности межколоночных связей через STDP

}

# загрузка MNIST

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,)), transforms.Lambda(lambda x: x.view(-1))])

train_set = datasets.MNIST(root='./data', train=True, download=True, transform=transform)

test_set = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

train_loader = DataLoader(train_set, batch_size=batch_size, shuffle=True, num_workers=4, pin_memory=True)

test_loader = DataLoader(test_set, batch_size=batch_size, shuffle=False, num_workers=4, pin_memory=True)

# создание модели

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

model = DynamicTopologyNetwork(**hyperparams).to(device)

# настройки обучения

optimizer = torch.optim.AdamW([

{'params': model.readout.parameters(), 'lr': learning_rate},

{'params': model.input_scale, 'lr': learning_rate * 0.05},

{'params': model.inter_weights, 'lr': learning_rate * 0.1}

], lr=learning_rate, weight_decay=weight_decay)

scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(

optimizer,

T_max=len(train_loader) * epochs,

eta_min=learning_rate * 0.01

)

# оценка производительности

@torch.no_grad()

def evaluate(model, loader, device):

model.eval()

correct = 0

total = 0

all_spike_rates = []

for x, y in loader:

x, y = x.to(device), y.to(device)

logits, spike_rates = model(x)

preds = logits.argmax(dim=1)

correct += (preds == y).sum().item()

total += y.size(0)

all_spike_rates.append(spike_rates.mean().item())

accuracy = correct / total

avg_spike_rate = sum(all_spike_rates) / len(all_spike_rates)

return accuracy, avg_spike_rate

# обучение внутри эпохи

def train_epoch(model, train_loader, optimizer, scheduler, device, epoch):

model.train()

epoch_loss = 0.0

correct = 0

total = 0

epoch_spike_rates = []

for batch_idx, (x, y) in enumerate(train_loader, start=1):

x, y = x.to(device), y.to(device)

optimizer.zero_grad(set_to_none=True)

logits, spike_rates = model(x, learn=True)

loss = F.cross_entropy(logits, y)

target_rate = model.target_rate

rate_loss = torch.mean((spike_rates - target_rate) ** 2)

total_loss = loss + 0.05 * rate_loss

total_loss.backward()

torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=0.5)

optimizer.step()

scheduler.step()

with torch.no_grad():

preds = logits.argmax(dim=1)

correct += (preds == y).sum().item()

total += y.size(0)

epoch_loss += loss.item()

epoch_spike_rates.append(spike_rates.mean().item())

if batch_idx % 100 == 0:

print(f'Epoch {epoch:02d} [{batch_idx:3d}/{len(train_loader)}] Loss={loss.item():.4f} Accuracy={(correct / total)*100:.2f}% LR={scheduler.get_last_lr()[0]:.6f}')

train_loss = epoch_loss / len(train_loader)

train_acc = correct / total

avg_spike_rate = sum(epoch_spike_rates) / len(epoch_spike_rates)

return train_loss, train_acc, avg_spike_rate

# цикл обучения

history = {'train_loss': [], 'train_acc': [], 'test_acc': [], 'spike_rates': []}

total_start = time.time()

for epoch in range(1, epochs + 1):

train_loss, train_acc, train_spike_rate = train_epoch(model, train_loader, optimizer, scheduler, device, epoch)

test_acc, test_spike_rate = evaluate(model, test_loader, device)

history['train_loss'].append(train_loss)

history['train_acc'].append(train_acc)

history['test_acc'].append(test_acc)

history['spike_rates'].append(test_spike_rate)

print(f"\nEpoch {epoch}/{epochs} - Train Loss: {train_loss:.4f} | Train Accuracy: {train_acc*100:.2f}% | Test Accuracy: {test_acc*100:.2f}%")

total_time = time.time() - total_start

# финальная оценка и сохранение

final_acc, final_spike_rate = evaluate(model, test_loader, device)

torch.save({

"epoch": epochs,

"model_state_dict": model.state_dict(),

"test_accuracy": final_acc,

"spike_rate": final_spike_rate,

"hyperparams": hyperparams,

"history": history,

"training_time": total_time

}, "DynamicTopologyNetwork.pth")

print(f"\nОбучение завершено за {total_time/60:.1f} мин")

print(f"Финальная точность: {final_acc*100:.2f}%")

Запустим 64 кортикальные колонки на 40 эпохах обучения: python train_spiking_brain.py

Каждые 100 шагов будут выводиться данные о текущем уровне обучения:

Epoch 01 [100/469] Loss=1.4257 Accuracy=46.41% LR=0.000500

Epoch 01 [200/469] Loss=0.8772 Accuracy=59.13% LR=0.000499

Epoch 01 [300/469] Loss=0.6398 Accuracy=65.66% LR=0.000499

Epoch 01 [400/469] Loss=0.6708 Accuracy=69.41% LR=0.000498

EPOCH 1/40 - Train Loss: 1.0290 | Train Accuracy: 71.49% | Test Accuracy: 69.99%

Epoch 02 [100/469] Loss=0.5339 Accuracy=83.44% LR=0.000496

Epoch 02 [200/469] Loss=0.4850 Accuracy=83.86% LR=0.000494

Epoch 02 [300/469] Loss=0.4401 Accuracy=84.17% LR=0.000492

Epoch 02 [400/469] Loss=0.5152 Accuracy=84.34% LR=0.000490

EPOCH 2/40 - Train Loss: 0.5100 | Train Accuracy: 84.44% | Test Accuracy: 83.30%

...

Epoch 20 [100/469] Loss=0.3904 Accuracy=92.73% LR=0.000007

Epoch 20 [200/469] Loss=0.2344 Accuracy=92.82% LR=0.000006

Epoch 20 [300/469] Loss=0.2745 Accuracy=92.76% LR=0.000005

Epoch 20 [400/469] Loss=0.2477 Accuracy=92.87% LR=0.000005

Epoch 20/40 - Train Loss: 0.2373 | Train Accuracy: 91.93% | Test Accuracy: 91.87%

...

Epoch 40 [100/469] Loss=0.0102 Accuracy=96.12% LR=0.000003

Epoch 40 [200/469] Loss=0.0089 Accuracy=96.63% LR=0.000002

Epoch 40 [300/469] Loss=0.0091 Accuracy=96.51% LR=0.000001

Epoch 40 [400/469] Loss=0.0072 Accuracy=96.87% LR=0.000002

Epoch 40/40 - Train Loss: 0.0056 | Train Accuracy: 97.14% | Test Accuracy: 96.02%

Обучение завершено за 387 мин. Финальная точность: 96.02%

Обучение на видеокарте потребляло менее 1 Gb видеопамяти и заняло 6.5 часов. Результат: 96.02% точности на тестовых образцах. Отличный результат на уровне современных традиционных моделей. Для результата в 98%+ необходимо обучить сеть на 100-150 эпохах, так как чем биологичнее сеть, тем дольше (больше эпох) её нужно обучать на обычном оборудовании.

Принципиальное отличие данной архитектуры от традиционных нейронных сетей — это способность работать с временем как с фундаментальным измерением обработки информации.

В обычных нейросетях время отсутствует: входные данные обрабатываются мгновенно, за один проход. Время там — это всего лишь индекс в последовательности.

Наша спайковая сеть работает иначе. Благодаря механизму STDP и спайковой динамике, она обрабатывает информацию через множество временных шагов (time_steps = 50). Каждый входной образ разворачивается во времени как паттерн спайков, и сеть анализирует не статическую картину, а динамический процесс:

• LIF-нейроны накапливают потенциал со временем, создавая временную интеграцию сигналов
• STDP отслеживает порядок активации колонок: если колонка B активируется сразу после колонки A, их связь усиливается (LTP); если наоборот — ослабляется (LTD)
• Временные следы (pre_trace, post_trace) запоминают недавнюю активность с экспоненциальным затуханием

Это означает, что сеть может различать паттерны не только по тому, какие колонки активны, но и по тому, когда и в каком порядке они активируются. Два одинаковых набора активных колонок, но с разным временным порядком их возбуждения, будут обработаны по-разному. По сути, время становится дополнительным кодирующим измерением. Сеть может обучаться временным закономерностям: последовательностям событий, ритмам, задержкам между сигналами. Это приближает её к принципам работы биологического мозга, где временная синхронизация нейронных ансамблей играет ключевую роль в кодировании и обработке информации.

Наша архитектура почти полностью биологична: спайковые нейроны, кортикальные колонки, пластичность связей, временная динамика. Однако два элемента остаются классическими анахронизмами — входной и выходной слои.

Входной слой — линейное преобразование пикселей в токи для LIF-нейронов — играет роль сетчатки глаза. Заменить его на биологически корректный вариант мы пока не можем: для этого нужны нейроморфные процессоры и специализированные камеры, способные генерировать настоящие временные спайки из светового потока. Это вопрос аппаратного обеспечения ближайшего будущего.

Выходной слой — другая история. Здесь мы вольны экспериментировать:

self.readout = nn.Sequential(

nn.Linear(num_columns * col_out, 512),

nn.ReLU(),

nn.Dropout(0.2),

nn.Linear(512, top_out)

)

Сейчас это обычный классический перцептрон. Он принимает богатейшую симфонию спайковых паттернов — результат работы десятков колонок, временных корреляций, динамической топологии — и редуцирует всё это многообразие к линейной комбинации весов. Это рабочий подход, но он создаёт концептуальный разрыв. Что если биологический мозг на финальном этапе принятия решений использует нечто принципиально иное?

Существует гипотеза, что сознание оперирует квантовыми эффектами: суперпозицией состояний, запутанностью, интерференцией амплитуд вероятности. От микротрубочек Пенроуза до квантовой когерентности в нейронных ансамблях — идея спорна, но не беспочвенна. Если она верна, наш классический readout — это бутылочное горлышко, где гаснут квантовые корреляции, недоступные детерминистической логике.

В следующей статье мы шагнём за эту границу. Заменим линейный классификатор на слой кубитов — квантовый интерпретатор, способный держать в суперпозиции одновременно все возможные интерпретации входного паттерна. Спайки станут квантовыми состояниями, а ответ сети родится из коллапса волновой функции при измерении.

Это звучит как научная фантастика, но квантовые процессоры и возможность их симуляции на обычных видеокартах уже реальность. Возможно, именно там, на квантовом уровне, скрывается тайна того, как паттерны возбуждения превращаются в осознанный опыт.

В следующей статье мы попробуем приоткрыть эту дверь.

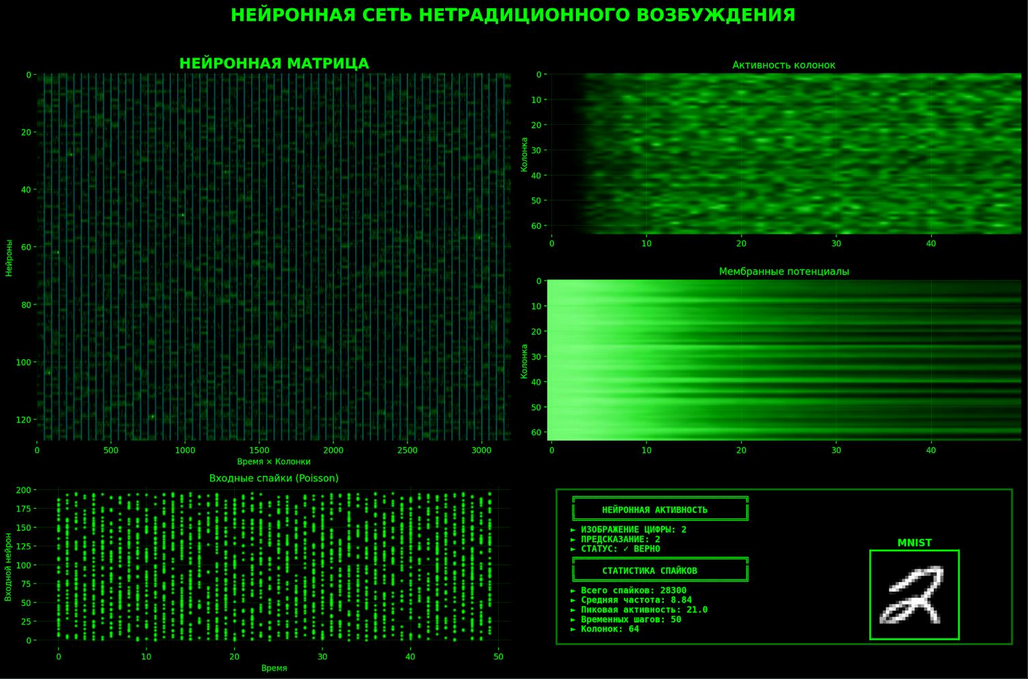
А пока обратите внимание на второе изображение. Оно показывает предсказания сети, которую мы только что обучили. Видно, что сеть справилась со всеми примерами, кроме одного, перепутав 5 с 6. Хотя, если честно, я тоже вижу 6. А что видите вы?

Литература

1. Obezyan et al., Нейронные сети нетрадиционной ориентации, LOR (2026)
2. P. Sosík et al., A survey on learning models of spiking neural membrane systems, Springer Nature (2025)
3. Y. Zhu, Cross-stimulus inhibition in trained SNNs, Springer Nature (2026)
4. M. Zhang et al., Bridging neuromorphic computing and deep learning for next-generation neural data interpretation, Frontiers in Computational Neuroscience (2026)
5. M. Hosseini et al., An organic spiking artificial neuron with excitatory and inhibitory synapses: towards soft and flexible organic neuromorphic processing, Nature (2026)
6. Q. Bai et al., A Brain‑Inspired Gating Mechanism Unlocks Robust Computation in SNNs, arXiv (2025)
7. Y. Huang et al., CogniSNN: Enabling Neuron-Expandability, Pathway-Reusability, and Dynamic-Configurability with Random Graph Architectures in Spiking Neural Networks, arXiv (2025)
8. O. Garcia-Palenciaet al., Spiking Neural Networks for Multimodal Neuroimaging: A Comprehensive Review of Current Trends and the NeuCube Brain-Inspired Architecture, mdpi (2025)