В этой статье вы узнаете, как разобрать арифметическое выражение в привычном формате из строки в структуру данных “дерево”, а затем путём обхода дерева вычислить выражение. Другими словами, мы пишем калькулятор.

У статьи есть пример на github, он написан в процедурном стиле на C++.

BNF-нотация арифметических выражений

Нас интересуют арифметические выражения без скобок и с пятью операторами:

• "+" - сложение
• "-" - вычитание
• "*" - умножение
• "/" - деление (получение частного от деления)
• "%" - деление по модулю (получение остатка от деления)

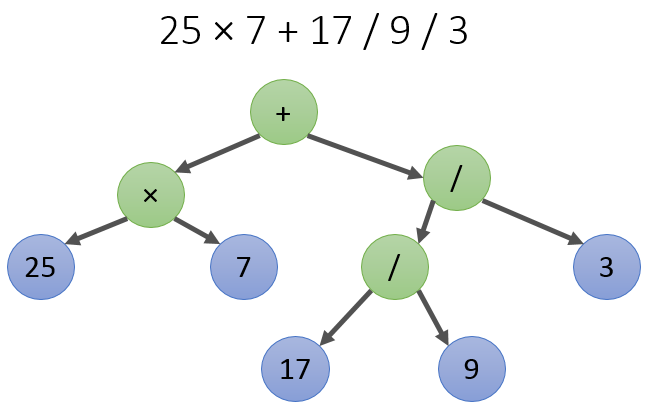
Примеры таких выражений:

12 / 12 / 12 => 0.0833333

25 + 17 / 45 / 2 => 25.1889

Синтаксис выражений можно описать в BNF-нотации (также известной как нотация Бекуса-Наура). Такая нотация ещё называется грамматикой, и выглядит как набор правил:

expression ::= add_sub_expr

add_sub_expr ::= mul_div_expr '+' add_sub_expr

| mul_div_expr '-' add_sub_expr

| mul_div_expr

mul_div_expr ::= atom_expr '*' mul_div_expr

| atom_expr '/' mul_div_expr

| atom_expr '%' mul_div_expr

| atom_expr

atom_expr ::= [0-9]+

Данная грамматика учитывает неравный приоритет операторов: в выражении 1 + 2 * 2 вы сначала должны свернуть 2 * 2 как mul_div_expr по правилу atom_expr '*' mul_div_expr, а потом уже свернуть 1 + mul_div_expr в add_sub_expr. Раскроем эту мысль подробнее с помощью пошаговой трассировки сворачивания правил грамматики:

1) 17 + 25 / 7

2) atom_expr + 25 / 7 # правило atom_expr ::= [0-9]+

3) atom_expr + atom_expr / 7 # правило atom_expr ::= [0-9]+

4) atom_expr + atom_expr / atom_expr # правило atom_expr ::= [0-9]+

5) mul_div_expr + atom_expr / atom_expr # правило mul_div_expr ::= atom_expr

6) mul_div_expr + atom_expr / mul_div_expr # правило mul_div_expr ::= atom_expr

7) mul_div_expr + mul_div_expr # правило mul_div_expr ::= atom_expr '/' mul_div_expr

8) mul_div_expr + add_sub_expr # правило add_sub_expr ::= mul_div_expr

9) add_sub_expr # add_sub_expr ::= mul_div_expr '+' add_sub_expr

Сверху вниз: строим и обходим дерево выражения

Дерево выражения — это вот такая прикольная штука:

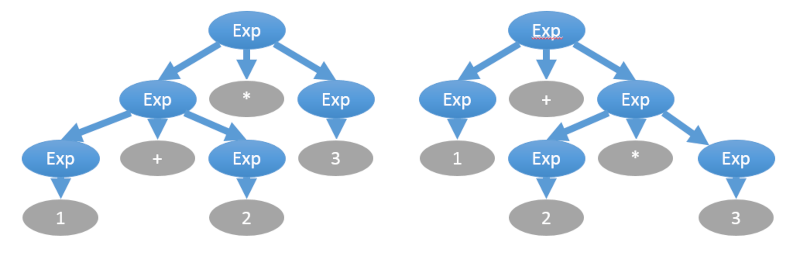
Способ превращения выражения в дерево зависит от приоритета операторов, который можно сменить расстановкой скобок. В качестве упражнения попробуйте восстановить тексты двух выражений, деревья которых нарисованы ниже:

Вычислить выражение по дереву легко и просто, достаточно обойти слева направо в глубину, применяя оператор в каждом нелистовом узле к дочерним узлам. Главный вопрос — как собрать дерево, имея строковое выражение?

Мы воспользуемся принципом нисходящего разбора, и применим нисходящий подход к проектированию программы. Сначала опишем функцию, которая получает выражение в виде строки и вычисляет его как число с плавающей точкой:

double Calculate(const std::string &expression)

{

Expression *pExpression = CreateExpression(expression);

const double result = CalculateExpression(pExpression);

DisposeExpression(pExpression);

return result;

}

Expression — это узел дерева. Интересно, что узел дерева сам является деревом, ведь дерево — это рекурсивное понятие, не так ли? В листьях дерева находятся

struct Expression;

// Expression tree node operation code.

enum class Operation

{

NOP, // just a value

ADD, // +

SUB, // -

MUL, // *

DIV, // /

MOD, // %

};

// Expression tree node is expression itself,

// since expressions are recursively defined.

struct Expression

{

double value = 0;

Operation op = Operation::NOP;

Expression *pLeft = nullptr;

Expression *pRight = nullptr;

};

Вычисление выражения по дереву:

double CalculateExpression(Expression *pExpr)

{

// Для листовых узлов возвращаем их численное значение

// если бы у нас была поддержка переменных, мы бы выполнили

// запрос значения переменной по имени в ассоциативном массиве переменных

if (pExpr->op == Operation::NOP)

{

return pExpr->value;

}

// Вычисляем выражения в левом и в правом поддеревьях

assert(pExpr->pLeft);

assert(pExpr->pRight);

CalculateExpression(pExpr->pLeft);

CalculateExpression(pExpr->pRight);

// Применяем операцию текущего узла

switch (pExpr->op)

{

case Operation::ADD:

pExpr->value = pExpr->pLeft->value + pExpr->pRight->value;

break;

case Operation::SUB:

pExpr->value = pExpr->pLeft->value - pExpr->pRight->value;

break;

case Operation::MUL:

pExpr->value = pExpr->pLeft->value * pExpr->pRight->value;

break;

case Operation::DIV:

pExpr->value = pExpr->pLeft->value / pExpr->pRight->value;

break;

case Operation::MOD:

pExpr->value = fmod(pExpr->pLeft->value, pExpr->pRight->value);

break;

case Operation::NOP:

assert(false);

break;

}

return pExpr->value;

}

Превращаем правила в функции

Мы хотим реализовать функцию Expression *CreateExpression(const std::string &expression);, которая выполняет разбор строки и в случае успеха возвращает указатель на выражение. Для этого на каждое из правил в BNF-нотации объявим по одной функции. Соглашения будут таковы:

• В случае успешного разбора функция возвращает Expression *, то есть стек вызовов функций уменьшается на одну запись
• В случае ошибки функция корректно удаляет выделенную память и выбрасывает исключение, то есть начинается экстренная раскрутка стека вызовов функций
• Функция может рекурсивно вызывать себя или другие функции
• Функция принимает изменяемую ссылку на строку, и в случае успешного разбора своего участка отсекает этот участок из строки, оставляя всё, что находится правее. Например, в выражении 18 - 7 после успешного разбора первого atom_expr подстрока “18” должна быть убрана из строки

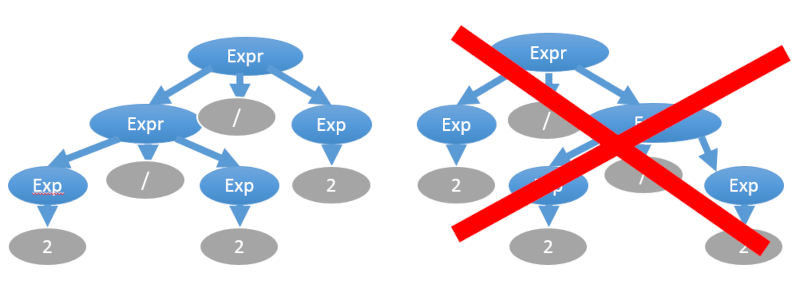
Expression *ParseAtom(std::string &str);

Expression *ParseMulDiv(std::string &str);

Expression *ParseAddSub(std::string &str);

В псевдокоде реализация разбора atom должна выглядеть так:

Expression *ParseAtom(std::string &str)

{

// Попытаться считать число.

// Если удалось, пропустить считанную часть str,

// создать Expression* и вернуть его.

// Иначе бросаем исключение

}

Наивная реализация разбора expr_mul_div могла бы выглядеть так:

Expression *ParseMulDiv(std::string &str)

{

// Попытаться считать atom (не удалось - бросаем исключение).

// Проверить, есть ли впереди оператор *, / или %

// если нет, возвращаем Expression* от atom

// если да, считываем и пропускаем оператор

// Попытаться считать atom (не удалось - бросаем исключение).

// Формируем Expression из двух atom и оператора

}

К сожалению, такая реализация не сможет разобрать выражение “abc”, в котором число операций одного уровня — 3 или более. Сразу заметим, что в разборе таких выражений надо учитывать жестокие правила ассоциативности, например, «2/2/2» правильно вычисляется как «(2/2)/2=0,5», а не «2/(2/2)=2»

Именно из-за левой ассоциативности деления такая реализация не подходит (но она подошла бы для правоассоциативных правил, таких как присваивание):

Expression *ParseMulDiv(std::string &str)

{

// Попытаться считать atom (не удалось - бросаем исключение).

// Проверить, есть ли впереди оператор *, / или %

// если нет, возвращаем Expression* от atom

// если да, считываем и пропускаем оператор

// Попытаться рекурсивно считать expr_mul_div (не удалось - бросаем исключение).

// Формируем Expression из atom, expr_mul_div и оператора

}

Если же попытаться при разборе expr_mul_div в первую очередь искать вложенный expr_mul_div, то будет очевидная бесконечная рекурсия и следующее за ней переполнение стека программы. Поэтому нам ничего не остаётся, кроме как заменить рекурсию на цикл, и на каждой итерации цикла присоединять уже собранный expr_mul_div к новому как левое поддерево.

Реализуем функции разбора

В реализациях этих функций мы применим три дополнительные функции, которые по тем же принципам отсекают от строки пробельные символы, число и следующий оператор соответственно:

void SkipSpaces(std::string &expression)

{

size_t numSize = 0;

while (numSize < expression.size()

&& (expression[numSize] == ' '))

{

++numSize;

}

expression = expression.substr(numSize);

}

// Skips spaces, then reads until first non-digit character.

// If successful, removes read characters from `expression`

// and returns true.

bool ParseDouble(std::string &expression, double &result)

{

std::string remainingStr = expression;

SkipSpaces(remainingStr);

size_t numSize = 0;

if (remainingStr.size() > 0 && isdigit(remainingStr[0]))

{

while (numSize < remainingStr.size()

&& isdigit(remainingStr[numSize]))

{

++numSize;

}

result = std::stod(remainingStr.substr(0, numSize));

expression = remainingStr.substr(numSize);

return true;

}

return false;

}

// Skips spaces, then reads next operator symbol.

// If successful, removes read characters from `expression`

// and returns true.

bool ParseOperator(std::string &expression, Operation &op)

{

std::string remainingStr = expression;

SkipSpaces(remainingStr);

if (remainingStr.empty())

{

op = Operation::NOP;

return false;

}

switch (remainingStr[0])

{

case '+':

op = Operation::ADD; break;

case '-':

op = Operation::SUB; break;

case '*':

op = Operation::MUL; break;

case '/':

op = Operation::DIV; break;

case '%':

op = Operation::MOD; break;

default:

op = Operation::NOP; break;

}

const bool succeed = (op != Operation::NOP);

if (succeed)

{

expression = remainingStr.substr(1);

}

return succeed;

}

Теперь можно показать, как выглядят реализации функций разбора по правилам грамматики. Не забываем о ранее запланированной замене рекурсии на цикл.

// Parses expressions like: `a`, `a+b±...`, `a-b±...`,

// where each sub-expression parsed by `ParseMulDiv`.

Expression *ParseAddSub(std::string &str)

{

Expression *left = ParseMulDiv(str);

while (true)

{

Operation op = Operation::NOP;

// Don't remove operator from remaining string

// when this operator remains unhandled.

std::string remainingStr = str;

if (!ParseOperator(remainingStr, op)

|| (op != Operation::ADD && op != Operation::SUB))

{

return left;

}

str = remainingStr;

Expression *right = nullptr;

try

{

right = ParseMulDiv(str);

}

catch (...)

{

DisposeExpression(left);

throw;

}

try

{

Expression *expr = new Expression;

expr->pLeft = left;

expr->pRight = right;

expr->op = op;

left = expr;

}

catch (...)

{

DisposeExpression(left);

DisposeExpression(right);

throw;

}

}

return left;

}

// Parses expressions like: `a`, `a*b...`, `a/b...`, `a%b...`

// where each sub-expression parsed by `ParseAtom`.

Expression *ParseMulDiv(std::string &str)

{

Expression *left = ParseAtom(str);

while (true)

{

Operation op = Operation::NOP;

// Don't remove operator from remaining string

// when this operator remains unhandled.

std::string remainingStr = str;

if (!ParseOperator(remainingStr, op)

|| (op != Operation::MUL && op != Operation::DIV && op != Operation::MOD))

{

return left;

}

str = remainingStr;

Expression *right = nullptr;

try

{

right = ParseAtom(str);

}

catch (...)

{

DisposeExpression(left);

throw;

}

try

{

Expression *expr = new Expression;

expr->pLeft = left;

expr->pRight = right;

expr->op = op;

left = expr;

}

catch (...)

{

DisposeExpression(left);

DisposeExpression(right);

throw;

}

}

return left;

}

// Parses atom expression, like a number.

Expression *ParseAtom(std::string &str)

{

Expression *expr = new Expression;

if (!ParseDouble(str, expr->value))

{

DisposeExpression(expr);

throw std::invalid_argument("Expected number at: " + str);

}

return expr;

}

Что смотреть дальше и что улучшить

Другие примеры и теоретические выкладки по рекурсивному спуску есть в сети:

• Recursive descent parser (en.wikipedia.org)
• Compiler Design - Top-Down Parser

В нашем парсере происходит множественное копирование строк в процессе разбора. Этого можно было бы избежать, если каждая рекурсивно вызываемая функция принимала бы string_view — невладеющую ссылку на строку. Реализацию string_view можно раздобыть несколькими способами:

1. Найти компилятор и IDE с поддержкой C++17, в котором <string_view> и объявленные в этом заголовке классы стали частью стандартной библиотеки
2. Взять тривиальную реализацию на Github, состоящую из одного заголовка: github.com/sergey-shambir/string_view
3. Получить Boost версии 1.61 или выше, в котором есть <boost/utility/string_view.hpp>

По сути string_view — это удобная замена такой вот структуры для чтения строки слева направо:

struct StringScanState

{

std::string text;

size_t position;

};

Упражнения

Перед кодированием составьте исправленную BNF-грамматику, чтобы спроектировать, как добавить новую возможность.

• Добавьте в парсер поддержку скобок вокруг выражения. При отсутствии закрывающей скобки парсер должен выдавать какую-либо ошибку.
• Добавьте в парсер поддержку чтения чисел с плавающей запятой, таких как 124.17. Для разбора вы можете использовать функцию double strtod(const char *nptr, char **endptr);, её полезная особенность — остановка разбора на первом недопустимом символе, с занесением адреса символа в endptr (подробнее см. документацию).
• Добавьте в парсер поддержку унарных операторов плюс и минус. Оператор может встретиться перед любым числом, но только в одиночку, т.е. выражения вида a * -1 допустимы, а выражения вида a + - - 2 — нет.