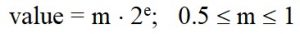Модуль math. Теоретико-числовые функции и функции представления

---

Содержание

• 1. Подключение модуля  math . Функция ceil() . Округление в большую сторону
• 2. Функция copysign(x,y) . Присваивание аргумента с учетом знака числа
• 3. Функция fabs(x) . Модуль числа
• 4. Функция  factorial(x) . Вычисление факториала
• 5. Функция  floor(x) . Округление в меньшую сторону
• 6. Функция fmod(x, y) . Остаток от деления
• 7. Функция frexp(x) . Вычисление нормализованной мантиссы и несдвинутого порядка числа
• 8. Функция fsum() . Сумма чисел в итерированном объекте
• 9. Функция gcd(a, b) . Наибольший общий делитель двух чисел
• 10. Функция isclose() . Определение близости чисел
• 11. Функция  isfinite(x) . Определение ограниченности
• 12. Функция  isinf(x) . Определение бесконечности
• 13. Функция  isnan(x) . Определение значения NaN (not a number)
• 14. Функция ldexp(x, i) . Обратная функция к  frexp(x)
• 15. Функция modf(x) . Выделение дробной и целой части вещественного числа
• 16. Функция remainder(x, y)  . Остаток  x  относительно y
• 17. Функция trunc(x) . Определение целой части числа
• Связанные темы

---

Поиск на других ресурсах:

1. Подключение модуля math. Функция math.ceil(). Округление в большую сторону

Чтобы использовать теоретико-числовые функции и функции представления из модуля math, нужно этот модуль предварительно подключить

import math

Функция math.ceil(x) возвращает такое вещественное число y, которое удовлетворяет следующим условиям:

• значение числа y равно ближайшему целому x;
• значение числа y больше или равно значению x.

В качестве аргумента x может задаваться только целое или вещественное число. Если попробовать задать комплексное число в качестве аргумента x, то интерпретатор сообщит об ошибке.

Пример.

import math

# для вещественного аргумента, положительные числа

x = 2.65

y = math.ceil(x) # y = 3.0

x = 3.0 # y = 3.0

y = math.ceil(x)

x = 2.000001

y = math.ceil(x) # y = 3.0

# вещественный аргумент, отрицательные числа

x = -2.0001 # y = -2.0

y = math.ceil(x)

# целочисленный аргумент

x = 13

y = math.ceil(x) # y = 13.0

  ⇑

2. Функция math.copysign(x,y). Присваивание аргумента с учетом знака числа

Функция math.copysign(x,y) возвращает результат вещественного типа, который равен значению аргумента x но со знаком аргумента y. Аргументы x, y могут быть только целого или вещественного типа.

Пример.

import math

# функция math.copysign(x,y)

x = 3.64

y = -5.44

z = math.copysign(x, y) # z = -3.64 => значение x, знак y

x = -2.85

y = 0.00001

z = math.copysign(x, y) # z = 2.85

# случай, когда y = -0.0

x = 2.85

y = -0.0 # вещественное отрицательное число

z = math.copysign(x, y) # z = -2.85

# случай, когда y = 0.0

x = 3.18

y = 0.0

z = math.copysign(x, y) # z = 3.18

  ⇑

3. Функция math.fabs(x). Модуль числа

Функция math.fabs(x) возвращает абсолютное значение аргумента x. Функция возвращает вещественный результат. Аргумент x может быть как вещестенного так и целого типа. Аргумент x не может быть комплексного типа.

Пример.

# функция math.fabs(x) - модуль x

import math

x = -15.55

y = math.fabs(x) # y = 15.55

x = 0.01

y = math.fabs(x) # y = 0.01

# для целого аргумента x

x = -15

y = math.fabs(x) # y = 15.0 - вещественный результат

---

---

  ⇑

4. Функция factorial(x). Вычисление факториала

Функция factorial(x) возвращает факториал целочисленногоаргумента x. Результат функции есть целого типа. Запрещено использовать аргумент x вещественного типа за исключением ситуаций, когда дробная часть равна 0 (например 5.0).

Пример.

# функция math.factorial(x)

import math

x = 5

y = math.factorial(x) # y = 120

x = 5.0 # разрешено, так как дробная часть равна 0

y = math.factorial(x) # y = 120

#x = 5.5 - Запрещено, ошибка

#y = math.factorial(x) # y = 120

  ⇑

5. Функция floor(x). Округление в меньшую сторону

Функция math.floor(x) возвращает вещественное число y, которое удовлетворяет следующим условиям:

• значение числа y равно ближайшему целому x;
• значение числа y меньше или равно значению x.

В качестве аргумента x может задаваться только целое или вещественное число. Если попробовать задать комплексное число в качестве аргумента x, то интерпретатор сообщит об ошибке.

Пример.

# функция math.floor(x)

import math

x = 5.2

y = math.floor(x) # y = 5.0

x = 5.99

y = math.floor(x) # y = 5.0

x = -5.2

y = math.floor(x) # y = -6.0

x = -6.0

y = math.floor(x) # y = -6.0

  ⇑

6. Функция math.fmod(x, y). Остаток от деления

Функция fmod(x,y) возвращает остаток от деления двух чисел. Каждый из аргументов x, y может быть целого или вещественного типа. Функция есть аналогом оператора %.
Разница между функцией fmod() и оператором % состоит в следующем. Для целочисленных аргументов оператор % возвращает результат целого типа. В то же время функция fmod(x, y) для аргументов целого типа возвращает результат вещественного типа.
Оператор % можно также применять для аргументов вещественного типа. Однако, в некоторых случаях оператор x%y может быть не совсем вычисляемым для вещественных аргументов. Поэтому этот оператор рекомендуется применять для целочисленных аргументов. А для вещественных аргументов лучше использовать функцию fmod(x, y).

Пример.

# функция math.fmod(x)

import math

# для вещестенных аргументов

x = 5.2

y = 0.4

y = math.fmod(x, y) # y = 0.3999999999999999

# для целочисленных аргументов

x = 15

y = 4

z = math.fmod(x, y) # z = 3.0 - вещественный результат

v = x % y # v = 3 - целочисленный результат

  ⇑

7. Функция math.frexp(x). Вычисление нормализованной мантиссы и несдвинутого порядка числа

Данная функция возвращает нормализованную мантиссу m и несдвинутый порядок e вещественного числа x в виде пары (кортежа). Вычислительные значения удовлетворяют соотношению:

Пример.

# функция math.frexpr(x)

import math

x = 2.8

y = math.frexp(x) # y = (0.7, 2)

# нулевое значение x

x = 0.0

y = math.frexp(x) # y = (0.0, 0)

  ⇑

8. Функция math.fsum(). Сумма чисел в итерированном объекте

Функция math.fsum(x) находит точную сумму чисел с плавающей запятой в итерированном объекте x. Функция предотвращает потерю точности путем отслеживания некоторых промежуточных частичных сумм.

Пример.

# функция math.fsum(x)

import math

y = math.fsum([0.02, 0.02, 0.02, 0.02, 0.02]) # y = 0.1

  ⇑

9. Функция math.gcd(a, b). Наибольший общий делитель двух чисел

Функция math.gcd(a,b) реализована в версиях Python 3.5 и выше. Данная функция возвращает наибольший общий делитель аргументов a, b. Если a и b отличны от нуля, то результат функции есть наибольшее число, на которое a и b делятся нацело.

Пример.

# функция gcd(a,b)

import math

a = 15

b = 5

c = math.gcd(a,b) # c = 5

a = 60

b = 40

c = math.gcd(a,b) # c = 20

a = -60

b = 24

c = math.gcd(a,b) # c = 12

  ⇑

10. Функция math.isclose(). Определение близости чисел

Данная функция используется в версиях Python 3.5 и выше.
Функция isclose(a, b, rel_tol, abs_tol) возвращает True, если числа a, b есть близкими один к одному по значению. В противном случае функция возвращает False.

Близость двух чисел вычисляется на основе:

• относительного допустимого отклонения rel_tol;
• абсолютного допустимого отклонения abs_tol.

Значения относительного и абсолютного отклонений могут быть заданы явно. Если значение относительного и абсолютного отклонений не заданы, то аргументы rel_tol и abs_tol принимают следующие значения:

• rel_tol = 1e-09;
• abs_tol = 0.0.

Если нужно задать относительную погрешность 3%, то rel_tol = 0.03.
Значение abs_tol определяет максимальный допуск между числами: abs_tol = |a-b|. Значение abs_tol может быть всегда не меньше нуля.

Пример.

# функция isclose(a,b,rel_tol,abs_tol)

import math

a = 5.000001

b = 5.0

c = math.isclose(a,b) # c = False

a = 5.0000000000001

b = 5.0

c = math.isclose(a,b) # c = True

  ⇑

11. Функция isfinite(x). Определение ограниченности

Функция isfinite(x) введена в версии Python 3.2 и выше. Данная функция возвращает True, если выполняются оба условия:

• значение x не является ограниченным;
• значение x не является равным NaN.

В другом случае функция возвращает False. Значение x = 0.0 рассматривается как ограниченное (конечное).

Пример.

# функция isfinite(x)

import math

x = 0.0

f = math.isfinite(x) # f = True

  ⇑

12. Функция isinf(x). Определение бесконечности

Функция isinf(x) возвращает True, если x есть ограниченной бесконечностью или отрицательной бесконечностью.

Пример.

# функция isinf(x)

import math

x = 0.0

f = math.isinf(x) # f = False

  ⇑

13. Функция isnan(x). Определение значения NaN (not a number)

Функция isnan(x) возвращает True, если значение x равно значению NaN (not a number). В другом случае функция возвращает False.
Значение NaN – это специальное значение (или состояние) которое принимает неопределенный результат. NaN возникает вследствие некоторых математических операций и не содержит никакого другого значения. NaN может возникать вследствие операций, которые дают неопределенный результат, например, деление ноль на ноль, умножение ноль на бесконечность и т.д.

Пример.

# функция isnan(x)

import math

x = 0.0/5

f = math.isnan(x) # f = False

  ⇑

14. Функция math.ldexp(x, i). Обратная функция к frexp(x)

Функция ldexp(x, i) возвращает значение x**(2*i). Функция есть обратной к функции math.frexp(x).

Пример.

# функция ldexp(x, i)

import math

x = 3.0

i = 2

y = math.ldexp(x,i) # y = 12.0

  ⇑

15. Функция math.modf(x). Выделение дробной и целой части вещественного числа

Функция math.modf(x) возвращает пару вещестенных чисел, которая состоит из:

• дробной части числа x (значение числа после запятой);
• целой части числа x.

Пример.

# функция modf(x)

import math

x = 3.23

y = math.modf(x) # y = (0.22999999999999998, 3.0)

x = -81.02

y = math.modf(x) # y = (-0.01999999999999602, -81.0)

  ⇑

16. Функция math.remainder(x, y) . Остаток x относительно y

Функция math.remainder(x, y) возвращает вещественное число, которое есть остаток x относительно y. Предполагается, что аргументы x и y есть ограниченными (finity). Также значение y может быть ненулевым.
Результат функции вычисляется по формуле

x – n · y

где n – ближайшее целое число к точному значению фактора x/y.

Пример.

# функция remainder(x,y)

import math

x = 3.2

y = 3.2

z = math.remainder(x, y) # z = 0.0

x = 3.7

y = 4.2

z = math.remainder(x, y) # z = -0.5

x = 4.7

y = 3.2

z = math.remainder(x, y) # z = 1.5

x = 15.0

y = 3.3

z = math.remainder(x, y) # z = -1.4999999999999991

x = -6.0

y = 2.1

z = math.remainder(x, y) # z = 0.30000000000000027

  ⇑

17. Функция math.trunc(x). Определение целой части числа

Функция math.trunc(x) возвращает целочисленное значение, которое равно целой части числа x.

Пример.

# функция trunc(x)

import math

x = 2.8

y = math.trunc(x) # y = 2

x = -3.001

y = math.trunc(x) # y = -3

x = 2.0000001

y = math.trunc(x) # y = 2

  ⇑

---

Связанные темы

• Степенные и логарифмические функции
• Тригонометрические функции
• Гиперболические функции
• Специальные функции и константы