Здесь представлена методичка Санкт-Петербургского политехнического университета Петра Великого от 2019 года "Высокопроизводительные вычисления с использованием пакета OpenFOAM". Методичка предназначена для студентов, обучающихся по направлению «Прикладные математика и физика».

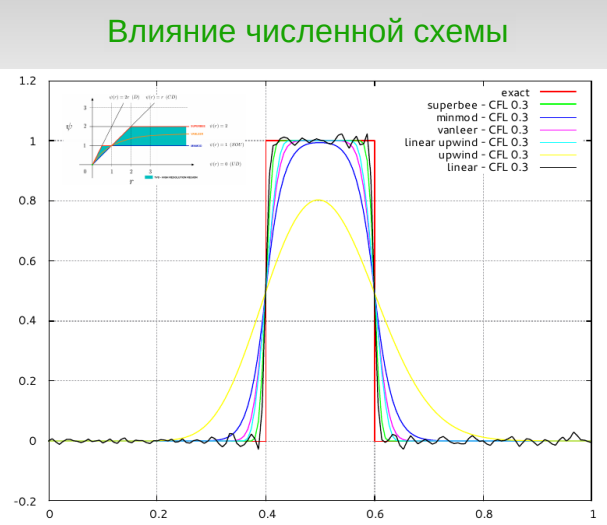
Методичка содержит 275 страниц формата A4.

В данной работе рассмотрены формулы и алгоритмы вычислений по теореме Гаусса-Остроградского и уравлениям Навье-Стокса. Имеются иллюстрации построения ячеек расчетной сетки. Описывается работа с пакетом OpenFOAM от установки до специфики использования, а так же рассказывается о сопровождающих вспомогательных программах ParaView и blockMesh. Так же есть пример создания и использования собственного решателя. Продемонстрировано использование OpenFOAM для расчета ламинарного и турбулентного течения.

Так же в методичке дано сравнение качества и точности расчетов в пакетах OpenFOAM и ANSYS Fluent на различных моделях и сетках по сравнению с результатами экспериментов.

В методичке рассматриваются следующие темы:

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1. Решение задач механики сплошных сред по методу

конечных объёмов . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.1. Предварительные замечания . . . . . . . . . . . . . . . . . . . 8

1.1.1. Скалярные, векторные и тензорные поля. Уравнения

физики для полевых величин . . . . . . . . . . . . . . . . . . . . . 8

1.1.2. Формулировка дифференциальных операторных уравнений

в интегральной форме, обобщённая теорема Гаусса-Остроградского . . . 12

1.1.3. Введение в численное моделирование . . . . . . . . . . . . . 14

1.2. Формулировка метода конечных объёмов (МКО) . . . . . . . . . . 17

1.2.1. Дискретизация расчётной области . . . . . . . . . . . . . . . 18

1.2.2. Ячейка расчётной сетки и дискретизация уравнения

в интегральной форме по МКО . . . . . . . . . . . . . . . . . . . . 21

1.2.3. Некоторые замечания о вычислении геометрических

параметров ячейки . . . . . . . . . . . . . . . . . . . . . . . . . 25

1.2.4. Вычисление дифференциальных операторов по МКО 28

1.3. Решение уравнений гидроаэродинамики по МКО . . . . . . . . . . 30

1.3.1. Дискретизация уравнения конвективно-диффузионного

переноса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

1.3.2. Аппроксимация временной производной . . . . . . . . . . . . . 39

1.3.3. Дискретизация уравнений Навье-Стокса . . . . . . . . . . . . 42

1.3.4. SIMPLE-подобные методы для решения задач динамики

несжимаемой жидкости . . . . . . . . . . . . . . . . . . . . . . . . 46

2. Общее описание пакета OpenFOAM в применении к

задачам механики сплошных сред 54

2.1. Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

2.2. Установка и структура OpenFOAM . . . . . . . . . . . . . . . . 56

2.2.1. Установка OpenFOAM в ОС на базе ядра Linux . . . . . . . . . 56

2.2.2. Структура пакета: основные каталоги . . . . . . . . . . . . . 61

2.2.3. Обзор основных решателей OpenFOAM . . . . . . . . . . . . . . 63

2.3. Пример постановки расчёта в OpenFOAM (задача

нестационарной теплопроводности) . . . . . . . . . . . . . . . . . . 65

2.3.1. Описание задачи . . . . . . . . . . . . . . . . . . . . . . . 65

2.3.2. Задание начальных и граничных условий . . . . . . . . . . . . 67

2.3.3. Задание управляющих параметров расчёта . . . . . . . . . . . 69

2.3.4. Запуск расчёта и мониторинг хода решения . . . . . . . . . . 72

2.3.5. Визуализация решения при помощи пакета ParaView . . . . . . . 76

2.4. Расчётная сетка в OpenFOAM . . . . . . . . . . . . . . . . . . 82

2.4.1. Формат сетки в OpenFOAM, типы границ . . . . . . . . . . . . 84

2.4.2. Создание сетки при помощи утилиты blockMesh . . . . . . . . . 89

2.4.3. Импорт из разных форматов и другие утилиты для

работы с сеткой . . . . . . . . . . . . . . . . . . . . . . . . . . 96

3. Решение задач гидроаэродинамики и теплообмена в

OpenFOAM (основные положения) 98

3.1. Численные схемы в OpenFOAM . . . . . . . . . . . . . . . . . . 98

3.1.1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . 98

3.1.2. Схемы вычисления диффузионных слагаемых . . . . . . . . . . . 102

3.1.3. Схемы интерполяции на грань . . . . . . . . . . . . . . . . . 104

3.1.4. Схемы вычисления градиента . . . . . . . . . . . . . . . . . 109

3.1.5. Аппроксимация временной производной . . . . . . . . . . . . . 110

3.1.6. Параметры решателей СЛАУ . . . . . . . . . . . . . . . . . . 112

3.1.7. Параметры алгоритмов . . . . . . . . . . . . . . . . . . . . 119

3.2. Граничные условия в OpenFOAM . . . . . . . . . . . . . . . . . 123

3.2.1. Предварительные замечания . . . . . . . . . . . . . . . . . . 123

3.2.2. Простейшие граничные условия в OpenFOAM . . . . . . . . . . . 128

3.2.3. Специальные граничные условия . . . . . . . . . . . . . . . . 131

3.2.4. Примеры постановки граничных условий . . . . . . . . . . . . 134

3.3. Дополнительные возможности . . . . . . . . . . . . . . . . . . 141

3.3.1. Инициализация и пост-обработка данных средствами

OpenFOAM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141

3.3.2. Обработка данных в ходе расчёта . . . . . . . . . . . . . . . 145

3.3.3. Библиотека расширений swak4foam . . . . . . . . . . . . . . . 149

4. Практикум по решению задач гидродинамики и теплообмена

в OpenFOAM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153

4.1. Ламинарные течения . . . . . . . . . . . . . . . . . . . . . . 153

4.1.1. Конвективный перенос скаляра однородным потоком . . . . . . . 153

4.1.2. Течение в начальном участке плоского канала . . . . . . . . . 162

4.1.3. Свободная конвекция в квадратной полости . . . . . . . . . . 167

4.2. Моделирование турбулентных течений на основе RANS-подхода . . . 178

4.2.1. Краткое введение в моделирование турбулентности . . . . . . . 179

4.2.2. RANS-модели в OpenFOAM . . . . . . . . . . . . . . . . . . . 184

4.2.3. Турбулентное течение в плоском канале . . . . . . . . . . . . 189

4.2.4. Течение и теплообмен за обратным уступом . . . . . . . . . . 200

5. Технология параллельных вычислений в OpenFOAM . . . . . . . . . . 215

5.1. Общие сведения о параллелизации . . . . . . . . . . . . . . . . 215

5.1.1. Предварительные замечания . . . . . . . . . . . . . . . . . . 215

5.1.2. Количественные измерения качества паралеллизации . . . . . . 217

5.2. Параллелизация в OpenFOAM . . . . . . . . . . . . . . . . . . . 220

5.2.1. Декомпозиция расчётной области . . . . . . . . . . . . . . . 220

5.2.2. Запуск решателя и «сборка» решения . . . . . . . . . . . . . 222

5.2.3. Пример расчёта с использованием параллелизации . . . . . . . 224

6. Программирование с использованием библиотек OpenFOAM.

Создание решателей . . . . . . . . . . . . . . . . . . . . . . . . . 234

6.1. Общие сведения об организации кода OpenFOAM . . . . . . . . . . 234

6.1.1. Уровни абстракций и иерархия классов . . . . . . . . . . . . 235

6.1.2. Математические примитивы . . . . . . . . . . . . . . . . . . 238

6.1.3. Работа с сеткой и полями физических величин . . . . . . . . . 240

6.1.4. Дискретизация пространственных операторов по явной

и неявной схемам. Составление уравнений . . . . . . . . . . . . . . 246

6.2. Создание собственного решателя . . . . . . . . . . . . . . . . 250

6.2.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . 250

6.2.2. Компиляция программы . . . . . . . . . . . . . . . . . . . . 252

6.2.3. Функция main() . . . . . . . . . . . . . . . . . . . . . . . 254

6.2.4. Инициализация переменных . . . . . . . . . . . . . . . . . . 256

6.2.5. Чтение параметров задачи из управляющих файлов . . . . . . . 257

6.2.6. Задание совокупности решаемых уравнений . . . . . . . . . . . 259

6.3. Пример расчёта с использованием собственного решателя . . . . . 260

6.3.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . 260

6.3.2. Результаты расчёта . . . . . . . . . . . . . . . . . . . . . 265

6.4. Дополнительные сведения . . . . . . . . . . . . . . . . . . . . 268

6.4.1. Отладка программы . . . . . . . . . . . . . . . . . . . . . . 268

6.4.2. Программируемые граничные условия . . . . . . . . . . . . . . 270

Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272

По данному курсу так же существуют учебные презентации, используемые в лекциях курса. Они расположены по адресу:

https://drive.google.com/drive/folders/1hQd8GHN564AQuHEfCxlBEpBBWOcmomSl

Методичка прикреплена к данной записи.