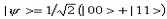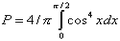|
|||||||
|
Структура реальности. Глава 2. Квантовые корреляции
Время создания: 07.06.2017 11:55
Текстовые метки: квантовая механика, объяснение
Раздел: Точные науки - Физика - Квантовая механика
Запись: xintrea/mytetra_syncro/master/base/1496825700fmbuzudzpi/text.html на raw.githubusercontent.com
|
|||||||
|
|
|||||||
|
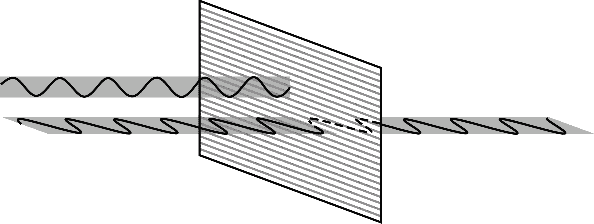
Если вы пошли в магазин за арбузом, то одновременно вы не можете находиться в кругосветном путешествии или на заседании ученого совета. Если арбуз оказался весом 8 кг, то ни у вас, ни у продавца не возникает сомнений в том, что как до взвешивания, так и после него его вес был именно 8 кг, а не 15 кг. Но Богом сотворенный мир гораздо богаче этого нашего житейского опыта… А. Белинский [15] Сейчас мы рассмотрим эксперименты, говорящие о наличии мгновенной связи между частицами на таких расстояниях, когда между ними уже нет никакого взаимодействия. Я не оговорился! Повторю еще раз: речь будет идти о мгновенной связи между частицами тогда, когда между ними нет никакого взаимодействия. Приступим. Известно, что фотоны, или кванты света, имеют такую характеристику, как поляризация, которая определяет направление колебаний электрического поля относительно направления движения фотона. Это схематично показано на рис. 5 — колебания волнообразной кривой, обозначающей электрическое поле фотона, лежат в некоторой плоскости, называемой плоскостью поляризации. Существуют пленочные покрытия, называемые поляризационными анализаторами, обладающие свойством пропускать кванты только с определенной плоскостью поляризации. Подобные пленки используются, например, в поляроидных очках, способных отфильтровывать всевозможные блики, поскольку отраженный свет частично поляризован. Я в таких очках люблю ходить на рыбалку — в них подводный мир виден как на ладони, поскольку почти весь отраженный от поверхности воды свет ими задерживается. Поляризующая пленка способна пропускать почти весь свет, когда он поляризован в некотором направлении, называемом оптической осью анализатора (она показана горизонтальными линиями). Фотон с такой поляризацией называют продольно поляризованным, он изображен на нижней части рисунка волнообразной линией. В то же время, пленка задерживает весь свет, поляризованный в направлении, перпендикулярном оптической оси поляризационного анализатора (волнообразная линия в верхней части рисунка). Такой фотон называют перпендикулярно поляризованным.
Рис. 5
В случае, когда плоскость поляризации фотона и оптическая ось анализатора образуют между собой угол [23] между 0 и 90°, нельзя дать определенного ответа на вопрос, пройдет фотон сквозь пленку или нет. Если кому интересно, в этом случае вероятность прохождения фотона будет равна квадрату косинуса указанного угла. Когда на пленку упадет фотон с поляризацией 45°, то исход события предсказать невозможно: при этом угле в среднем половина фотонов пройдет сквозь пленку, а половина будет задержана. Примерно половина фотонов будет проходить и в том случае, когда угол между плоскостью поляризации пучка и оптической осью анализатора случаен, как это имеет место при обычном дневном свете.
[23] В принятой формулировке — когда фотон линейно поляризован под некоторым углом между 0 и 90° к оптической оси анализатора.
В случае, когда поляризация пучка неопределенна, то есть когда продольные и поперечные компоненты поляризации пучка находятся в состоянии суперпозиции, волновой вектор падающего фотона имеет вид
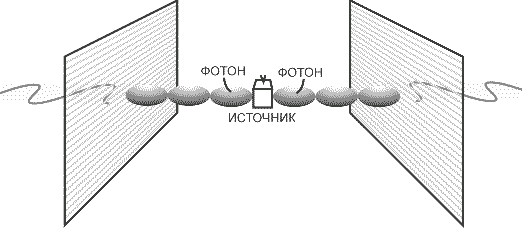
где |0> и |1> — компоненты, обозначающие продольную (то есть вдоль оптической оси) и поперечную (перпендикулярно к ней) поляризацию соответственно, а В этой непредсказуемости результата нет ничего странного, разве что может возникнуть вопрос: а уверены ли мы в том, что прохождение фотона сквозь поляризационный анализатор действительно есть случайный процесс? Может быть, есть какой-нибудь скрытый фактор, который определяет, пройдет ли фотон или нет, а мы его просто не знаем? К этому вопросу — вопросу о наличии так называемых скрытых параметров — мы вернемся позже, а пока попытаемся узнать, что происходит при одновременном наблюдении пары фотонов. Обычный источник света испускает фотоны со случайной поляризацией, и при наблюдении за любой парой таких фотонов мы увидим, что они будут вести себя совершенно независимо друг от друга. Однако в физике известны процессы, к примеру, последовательное испускание фотонов некоторыми атомами, находящимися в возбужденном состоянии, когда получаются два фотона с одинаковой поляризацией. Одно состояние — продольная поляризация обоих фотонов, другое возможное состояние — их поперечная поляризация. Поместим источник пар фотонов (в реальных экспериментах в качестве источника использовались атомы кальция и ртути) между двух поляризационных анализаторов (рис. 6), оптические оси которых параллельны, и понаблюдаем за прохождением каждого фотона из пары.
Рис. 6
Чтобы задать вектор состояния пары фотонов, необходимо описать состояния каждого из фотонов пары. Обозначения в квантовой механике приняты такие: внутри значка вектора |> первый символ описывает состояние первой частицы, а второй символ характеризует состояние второй частицы. Напомним, что источник выбран так, что вылетающие из него фотоны имеют одинаковую поляризацию. Обозначим как 0 состояние, когда фотон поляризован вдоль оси анализатора, и за 1 примем обозначение поляризации фотона перпендикулярно оптической оси. Возможны только два состояния фотонов пары — |00>, когда они оба поляризованы параллельно оптической оси, и |11>, когда оба они поляризованы перпендикулярно к ней. Соответственно, суперпозиция этих компонент описывается выражением
где |00> и |11> — компоненты, обозначающие продольную и поперечную поляризацию фотонов пары соответственно, а Первое, что нам необходимо проверить, это действительно ли поляризация каждого из фотонов пары случайна. Проделав соответствующие опыты, мы убеждаемся, что да: сквозь анализатор как справа, так и слева от источника проходит, в пределах статистической погрешности, ровно половина фотонов. Точно такой же результат мы бы имели при использовании любого обычного источника света. Далее следует проверить, что происходит, например, со вторым фотоном, когда первый поглощается. Согласно классическим представлениям, связь между ними должна быть, но только статистическая. Расчеты в теории вероятностей показывают, что при поглощении первого фотона поляризующей пленкой, второй с вероятностью 75% поглощается [24] , однако может с вероятностью 25% пройти сквозь пленку. В этих расчетах мы исходили из совершенно разумных, на первый взгляд, предположений о том, что оба фотона имеют определенную и совпадающую между собой поляризацию с момента своего рождения. [24] Эта вероятность определяется выражением:
Эксперимент же показывает, что если проходит один фотон, то всегда проходит и другой. А если поглощается один, то всегда поглощается и другой. То есть один из фотонов пары непостижимым образом знает, что происходит со вторым фотоном! Это происходит вне зависимости от расстояния между источником пар фотонов и анализаторами. Один из анализаторов, к примеру, может стоять рядом с источником, а второй — быть удален сколь угодно далеко. Полученный результат не зависит и от ориентации оптических осей анализаторов относительно горизонта: важно только, чтобы они совпадали. Возникает вопрос, можно ли использовать квантовые корреляции для «мгновенной» передачи классической информации из одной точки в другую? Ответ отрицателен, поскольку определяемые состояния частиц на каждом из анализаторов случайны, и их последовательность не несет никакой информации. Квантовая теория объясняет результат эксперимента поразительно просто и красиво: до измерения поляризации фотона, то есть до прохождения фотоном анализатора, состояния поляризации существуют в состоянии суперпозиции, их просто не существует как локальных характеристик частицы. А в ходе измерения анализатор выделяет из суперпозиции, определяемой выражением (3) либо компоненту |00>, либо компоненту |11>. И в том, и в другом случае оба фотона имеют одинаковую поляризацию, определяемую относительно оптической оси анализатора, поглотившего первый из фотонов! Соответственно, либо они оба будут поглощены, либо они оба пройдут сквозь пленки. Последнее утверждение справедливо, однако, лишь в том случае, когда оптические оси обоих анализаторов совпадают. Эта ситуация немного напоминает случай, когда у нас имелись два шара, черный и белый, которые потерялись. Найдя белый шар, мы можем утверждать, что оставшийся — черный. Однако объяснить поведение квантовых частиц в предположении, что каждый шар изначально белый или черный, не удастся. Шары, пока мы их не нашли, будут находиться в состоянии суперпозиции белого и черного и вести себя как бесцветные. И только тогда, когда мы определили цвет одного из шаров как черный, другой немедленно перестает быть бесцветным и приобретает белый цвет, на каком бы расстоянии он ни находился! А пока мы не увидели один из шаров, проведя тем самым измерение, шары не имеют цвета в качестве своей индивидуальной локальной характеристики. На первый взгляд, результаты эксперимента говорят, что квантовый объект каким-то непостижимым образом «узнает», что происходит с другим объектом, удаленным от него на значительное расстояние (сейчас проведены эксперименты с расстоянием между парами фотонов более 100 км). Это не совсем так: ничего никому не нужно узнавать, поскольку пара фотонов остается единым объектом по поляризационным (= спиновым [25] ) степеням свободы, несмотря на то, что «носители» поляризации пространственно разделены. Сложная система может быть локальна (то есть сепарабельна, разделима на независимые части) по одним степеням свободы и нелокальна (несепарабельна, неразделима на части) — по другим.
[25] Спин — собственный момент количества движения частицы. Двум возможным состояниям поляризации фотона отвечает проекция спина вдоль и против направления его движения.
Таким образом, в общем случае поляризационные свойства группы фотонов нельзя разделить и приписать каждому фотону свою, присущую ему и только ему поляризацию. Поляризация оказывается системным свойством, а не свойством отдельной частицы! То же самое можно сказать и о любых других характеристиках любой другой частицы или более сложного объекта. Подобную связь между частицами называют квантовыми корреляциями, а состояния участвующих в них частиц — запутанными. Запутанное состояние — состояние составной системы, которая не может быть разделена на отдельные, полностью самостоятельные и независимые части, то есть это несепарабельное (неразделимое) состояние.
Запутанные (это устоявшийся термин, хотя я бы предпочел термин «сцепленные») состояния могут возникать в системе, части которой взаимодействовали, а затем система распалась на невзаимодействующие друг с другом подсистемы. Например, если электрон сталкивается с атомом, то образуется запутанное состояние, в котором состояние электрона будет коррелированно с состоянием атома в результате произошедшего взаимодействия. Запутанное состояние не может быть представлено в виде совокупности состояний отдельных частей системы в силу наличия корреляций [26] между ними.
[26] То есть взаимной связи.
Суперпозиционные состояния — более общее понятие, чем запутанные состояния. В них компоненты волновой функции могут быть как коррелированны между собой, так и нет. Последний случай отвечает наличию в системе изолированных (сепарабельных) подсистем, которые никогда не взаимодействовали друг с другом. Сепарабельные подсистемы могут рассматриваться как существующие независимо друг от друга, они не запутаны между собой. Термины «несепарабельность», «запутанность» и «нелокальность» очень близки и означают наличие в системе квантовых корреляций.
Не беспокойтесь, если термины не сразу станут привычными, это нисколько не будет мешать восприятию дальнейшего повествования [27] .
[27] Напоминаем, что в конце книги приводится словарь основных терминов.
Наличие квантовых корреляций — неотъемлемое свойство запутанных состояний. Запутанные состояния частиц означают наличие связи между характеристиками этих частиц после их взаимодействия, в замкнутых системах связь между ними будет сохраняться всегда. А в случае открытых систем связь между частицами будет сохраняться до тех пор, пока суперпозиция состояний не превратится под влиянием взаимодействия с окружающими объектами в смесь. То есть смешанные состояния возникают как результаты измерений, выполненных над чисто-квантовыми состояниями, это результат декогеренции чисто-квантовых состояний (говорят — чистых состояний). Смешанные состояния — наиболее привычные для здравого смысла состояния, это именно та материя, которая воспринимается нашими органами чувств и классическими устройствами.
*****
В следующей главе речь пойдёт о нелокальности, детерминизме, мысленных опытах Эйншейна и решающих экспериментах, ответивших на вопрос, как устроен мир . [15] Белинский А. В . Квантовая нелокальность и отсутствие априорных значений измеряемых величин в экспериментах с фотонами // УФН. Т. 173. № 8. С. 905 (2003). Публикации из журнала «Успехи физических наук» можно найти на сервере http://www.ufn.ru/russian/main_r.html. |
|||||||
|
Так же в этом разделе:
|
|||||||

|
|||||||
|
|||||||
|

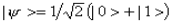 , (2)
, (2)