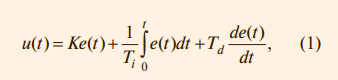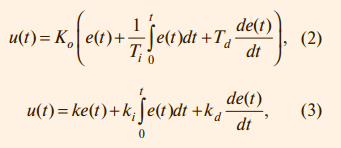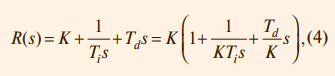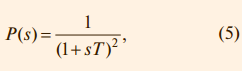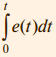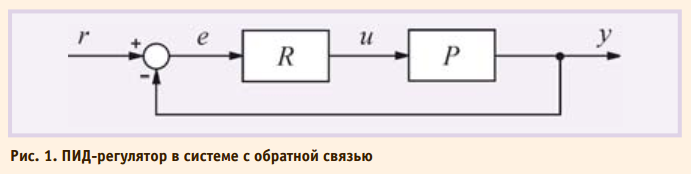
ВВЕДЕНИЕ

ПИД-регулятор был изобретён ещё в 1910 году [1]. Через 32 года, в 1942 году, Зиглер и Никольс разработали методику его настройки [2]. После появления микропроцессоров в 1980х годах развитие ПИД-регуляторов происходит нарастающими темпами. Общее количество публикаций по ПИД-регуляторам за 9 лет с 1973 по 1982 год составило 14 шт., с 1983 по 1992 год – 111 шт., а за период с 1998 по 2002 год (всего за 4 года) – 225 шт. [3]. На одном только семинаре IFAC (International Federation of Automatic Control) в 2000 году было представлено около 90 докладов, посвящённых ПИДрегуляторам [4]. Количество патентов по этой теме, содержащихся в патентной базе данных http://gb.espacenet.com, в январе 2006 года составило 364 шт.

ПИД-регулятор относится к наиболее распространённому типу регуляторов. Порядка 90-95% регуляторов [1, 5], находящихся в настоящее время в эксплуатации, используют ПИД-алгоритм. Причинами столь высокой популярности являются простота построения и промышленного использования, ясность функционирования, пригодность для решения большинства практических задач и низкая стоимость. Среди ПИД-регуляторов 64% приходится на одноконтурные регуляторы и 36% – на многоконтурные [6]. Контроллеры с обратной связью охва тывают 85% всех приложений, контроллеры с прямой связью – 6%, и контроллеры, соединённые каскадно, – 9% [6].

После появления дешёвых микропроцессоров и аналогоцифровых преобразователей в промышленных ПИД-регуляторах используются автоматическая настройка параметров, адаптивные алгоритмы, нейронные сети, генетические алгоритмы, методы нечёткой логики. Усложнилась структура регуляторов: появились регуляторы с двумя степенями свободы, с применением принципов разомкнутого управления в сочетании с обратной связью, со встроенной моделью процесса. Кроме функции регулирования, в ПИД-контроллер были введены функции аварийной сигнализации, контроля разрыва контура регулирования, выхода за границы динамического диапазона и др.

Несмотря на долгую историю развития и большое количество публикаций, остаются проблемы в вопросах устранения интегрального насыщения, регулирования объектов с гистерезисом и нелинейностями, автоматической настройки и адаптации. Практические реализации ПИД-контроллеров не всегда содержат антиалиасные фильтры, чрезмерный шум и внешние возмущения затрудняют настройку параметров. Проблемы усложняются тем, что в современных системах управления динамика часто неизвестна, регулируемые процессы нельзя считать независимыми, измерения сильно зашумлены, нагрузка непостоянна, технологические процессы непрерывны.

Далее рассмотрены только регуляторы для одномерных объектов (с одним входом и одним выходом), для медленных (тепловых) процессов, которые наиболее распространены в АСУ ТП.

КЛАССИЧЕСКИЙ ПИД-РЕГУЛЯТОР

Простейшая система автоматического регулирования с обратной связью показана на рис. 1. В ней блок R называют регулятором, P – объектом регулирования, r – управляющим воздействием, или уставкой, e – сигналом рассогласования, или ошибки, u – выходной величиной регулятора, y – регулируемой величиной.

Если выходная переменная u регулятора R описывается выражением:

где t – время, а K, Ti, Td – пропорциональный коэффициент, постоянная интегрирования и постоянная дифференцирования соответственно, то такой регулятор называют ПИДрегулятором.

В частном случае пропорциональная, интегральная или дифференциальная компоненты могут отсутствовать, и такие упрощённые регуляторы называют И, П, ПД или ПИ-регуляторами.

Распространены также следующие модификации выражения (1):

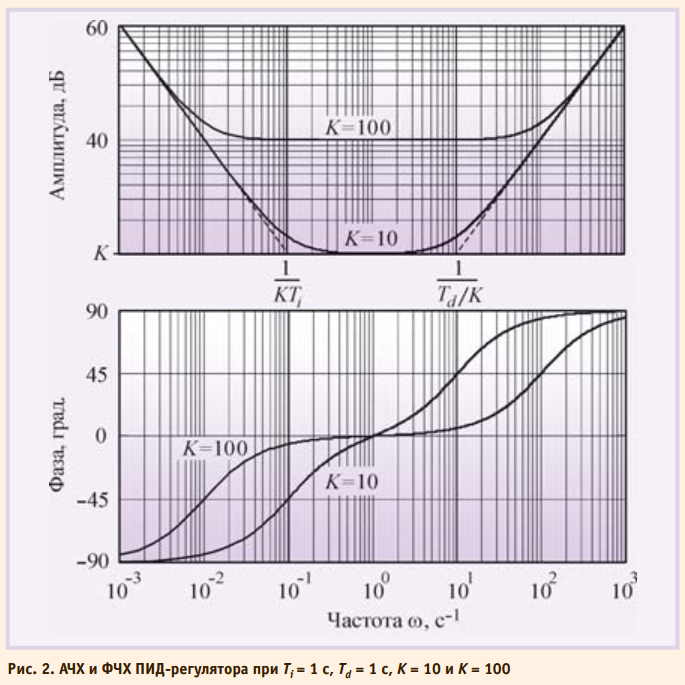
Между параметрами, входящими в выражения (1)-(3), существует простая связь. Однако отсутствие общепринятой системы параметров часто приводит к путанице. Это нужно помнить при замене одного ПИД-контроллера на другой или использовании программ настройки параметров. Мы будем пользоваться выражением (1).

Используя преобразование Лапласа при нулевых начальных условиях, передаточную функцию ПИД-регулятора можно представить в операторной форме:

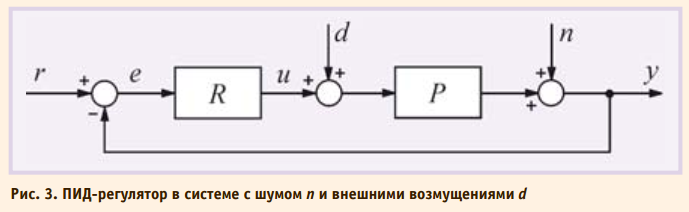
где s – комплексная частота.

Амплитудно-частотная (АЧХ) и фазочастотная (ФЧХ) характеристики операторной передаточной функции (4) показаны на рис. 2. В области нижних частот АЧХ и ФЧХ определяютсяинтегральным членом, в области средних частот – пропорциональным, в области высоких – дифференциальным.

На систему автоматического регулирования могут воздействовать (рис. 3) внешние возмущения d = d(s) и шум измерений n = n(s). Внешние возмущения (влияние нагрузки, изменение температуры окружающей среды, ветер, течение воды и т.п.) обычно пространственно распределены по объекту, однако для упрощения анализа их моделируют сосредоточенным источником d(s), приложенным ко входу системы. Источник шума n(s) моделирует погрешность измерений выходной переменой y, погрешность датчика, а также помехи [7, 8], воздействующие на канал передачи сигнала с выхода системы на её вход.

Вид АЧХ и ФЧХ регулятора определяет его точность и запас устойчивости. С уменьшением интегральной составляющей Ti, как следует из рис. 2, увеличивается модуль коэффициента усиления регулятора на низких частотах (то есть при приближении к установившемуся режиму), и поэтому снижается погрешность e.

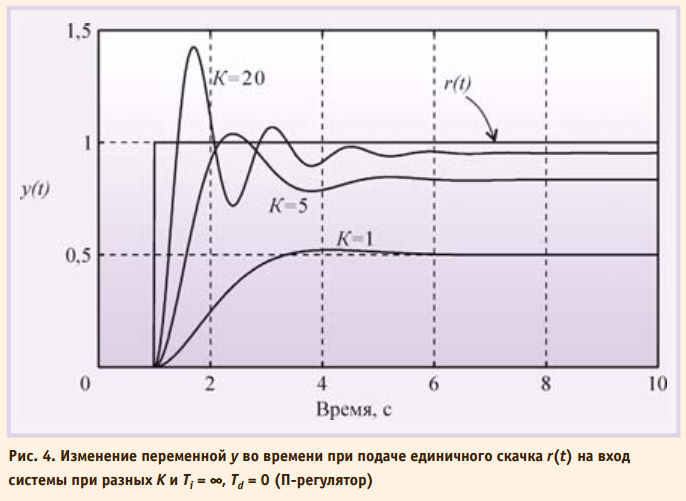
С увеличением дифференциальной составляющей Td растёт усиление на высоких частотах, что приводит к усилению шумов измерений и внешних возмущений. Поэтому дифференциальную составляющую используют только для улучшения формы переходного процесса в системе, а её практическая реализация обычно содержит фильтр высоких частот.

С ростом пропорционального коэффициента K увеличиваются модуль петлевого усиления контура регулирования и точность во всём диапазоне частот, однако падает запас по фазе и усилению, что ухудшает робастность и качество регулирования системы, а при дальнейшем увеличении K (рис. 4) возникают периодические колебания (система теряет устойчивость). Влияние шума и помех измерений n также уменьшается с ростом петлевого усиления и пропорционального коэффициента.

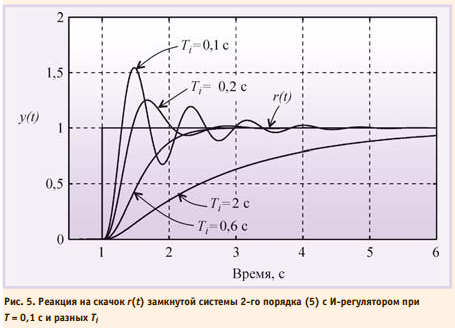
На рис. 5 показаны переходные характеристики замкнутой системы с И-регулятором (то есть при K = 0, Td = 0) и объектом второго порядка с переда точной функцией

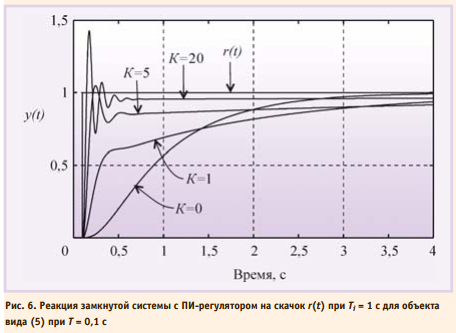
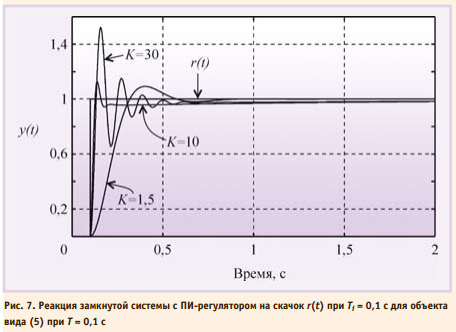
где T = 0,1 с. При больших постоянных интегрирования Ti переходная характеристика имеет вид, сходный с характеристикой апериодического звена. С уменьшением Ti растёт усиление регулятора, и когда на некоторой частоте петлевое усиление контура с обратнойсвязью приближается к 1, в системе появляются колебания.

АЧХ ПИ-регулятора можно получить из рис. 2, если отбросить правую ветвь АЧХ с наклоном +20 дБ/дек. При этом

сдвиг фаз на частотах выше 1 Гц не превысит уровень 0°. Таким образом, ПИ-регулятор имеет два существенных положительных отличия от И-регулятора: во-первых, его усиление на всех частотах не может стать меньше K, следовательно, увеличивается динамическая точность регулирования; во-вторых, по сравнению с И-регулятором он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент K не станет настолько большим, что увеличит усиление контура до еди ницы на частоте сдвига фаз 180° (ω180).

Переходный процесс в ПИ-регуляторе при разных сочетаниях Ti и K показан на рис. 6 и 7. При K = 0 (рис. 6) получаем И-регулятор. С ростом пропорционального коэффициента K появляется дополнительная ошибка во время переходного процесса (см. также рис. 4), которая при дальнейшем увеличении K уменьшается, однако при этом снижается запас устойчивости системы, поскольку с ростом K увеличивается усиление на частоте ω180. Это приводит к появлению затухающих колебаний в начале переходного процесса (рис. 6). Когда величина K становится достаточно большой для компенсации ослабления сигнала в объекте на частоте ω180, в системе появляются незатухающие колебания.

Пропорциональный коэффициент приводит к увеличению времени уста новления переходного процесса по уровню 0,99 по сравнению с И-регулятором при тех же Ti и T (рис. 6): с ростом K уменьшается наклон кривой y(t) при больших t; в частности, при t = 4 с кривая K = 1 проходит ниже кривой K = 0, а кривая K = 5 проходит ещё ниже. Объясняется это следующим. Уменьшение ошибки e в ПИ-регуляторе достигается действием одновременно как пропорционального, так и интегрального коэффициентов. Однако пропорциональный коэффициент не может свести ошибку к нулю (рис. 4). Поэтому оставшаяся ошибка e(t) уменьшается с течением времени при помощи члена

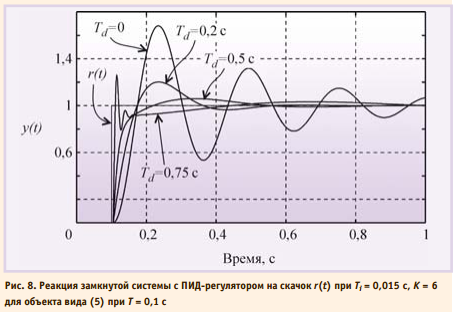
который нарастает тем медленнее, чем меньше e(t). В итоге введение пропорционального коэффициента, уменьшающего e(t), приводит к затягиванию переходного процесса.

В частотной области этот процесс можно объяснить тем, что с ростом K нуль передаточной функции 1/KTi смещается влево (рис. 2), то есть расширяется область частот, где интегральная составляющая пренебрежимо мала и ПИ-регулятор вырождается в чистый П-регулятор, которому свойственна ошибка в установившемся режиме.

В ПИД-регуляторе присутствует дифференциальный член, который, как следует из рис. 2, вносит положительный фазовый сдвиг до 90° на частотах выше K/Td. Это позволяет обеспечить устойчивость или улучшить качество регулирования системы в случаях, когда это невозможно сделать с помощью ПИ-регулятора. На рис. 8 показано влияние постоянной дифференцирования на форму отклика замкнутой системы на скачок r(t). Уменьшение амплитуды колебаний и увеличение коэффициента затухания с ростом постоянной дифференцирования Td объясняется тем, что благодаря положительному наклону АЧХ в области ω > K/Td (рис. 2) уменьшаются сдвиг фаз в контуре регулирования и петлевое усиление.

Дальнейшее увеличение постоянной дифференцирования приводит у росту усиления ПИД-регулятора на высоких частотах при ω > K/Td (рис. 2). Поскольку фазовый сдвиг, связанный с транспортной задержкой, неограниченно увеличивается с ростом частоты, то в системе даже с небольшой транспортной задержкой при увеличении Td всегда наступает момент, когда петлевое усиление на частоте фазового сдвига 180° превысит единицу. При этом на переходной характеристике замкнутой системы сначала появляются затухающие колебания (рис. 8, кривая Td = 0,75 с), затем при дальнейшем увеличении Td система переходит в колебательный режим.

Таким образом, с ростом постоянной дифференцирования запас устойчивости замкнутой системы сначала увеличивается, затем падает.

Продожение в следующем разделе.